ГОСТ Р 57639-2017 Пожарно-технический анализ. Часть 1. Валидация и верификация методов расчета

ГОСТ Р 57639-2017
(ИСО 16730-1:2015)

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

ПОЖАРНО-ТЕХНИЧЕСКИЙ АНАЛИЗ

Часть 1

Валидация и верификация методов расчета

Fire safety engineering. Part 1. Validation and verification of calculation methods

ОКС 13.220.01

Дата введения 2018-06-01

Предисловие

1 ПОДГОТОВЛЕН Обществом с ограниченной ответственностью "СИТИС" (ООО "СИТИС") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 274 "Пожарная безопасность"

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 5 сентября 2017 г. N 1009-ст

4 Настоящий стандарт является модифицированным по отношению к международному стандарту ИСО 16730-1:2015* "Пожарно-технический анализ. Процедуры и требования к верификации и валидации методов расчета. Часть 1. Общие положения" (ISO 16730-1:2015 "Fire safety engineering - Procedures and requirements for verification and validation of calculation methods - Part 1: General", MOD) путем изменения отдельных фраз (слов, значений, показателей), которые выделены в тексте курсивом**.

________________

* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей;

** В оригинале обозначения и номера стандартов и нормативных документов в разделах 2 "Нормативные ссылки", 5 "Методика", Приложении D и отмеченные в разделе "Предисловие" знаком "**" выделены курсивом, остальные по тексту документа приводятся обычным шрифтом. - Примечания изготовителя базы данных.

Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).

Сведения о соответствии ссылочных национальных стандартов международным стандартам, использованным в качестве ссылочных в примененном международном стандарте, приведены в дополнительном приложении ДА

5 ВВЕДЕН ВПЕРВЫЕ

6 ПЕРЕИЗДАНИЕ. Ноябрь 2019 г.

Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации"**. Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)

Введение

Цель пожарно-технического анализа заключается в оказании помощи в достижении приемлемого расчетного уровня пожарной безопасности. Кроме того, в настоящем стандарте описано использование методов расчета для того, чтобы:

- прогнозировать ход событий, которые потенциально могут иметь место в случае пожара или в его результате;

- оценивать возможности противопожарной защиты по снижению воздействия неблагоприятных последствий пожара на людей, имущество, окружающую среду и другие объекты.

Основные принципы, которые необходимы для обеспечения надежности этих методов расчета, - верификация и валидация.

В настоящем стандарте в общих чертах рассмотрены оценка, верификация и валидация методов расчета пожарно-технического анализа.

Потенциальные пользователи методов расчета и лица, ответственные за принятие полученных результатов, должны быть уверены в том, что методы расчета обеспечивают достаточно точные прогнозы течения и последствий пожара в каждом конкретном случае. В связи с чем необходимо, чтобы выбранные методы расчета прошли верификацию на предмет математической точности и валидацию на способность воспроизводить эти процессы. Тщательно проводимый процесс валидации и верификации является ключевым элементом обеспечения качества проделанной работы.

Не существует четко установленного требования к точности, применимого ко всем методам расчета, так как уровень точности зависит от цели использования метода расчета. Причем не все методы расчета должны демонстрировать высокую точность при наличии выявленных ошибок, неопределенностей и ограничений применимости.

Предметом настоящего стандарта является точность прогнозирования методов расчета. Однако и другие факторы, такие как удобство использования, актуальность, завершенность и статус разработки, играют важную роль в оценке применения наиболее подходящего метода расчета в каждом конкретном случае. Оценка пригодности метода расчета для специального назначения в области пожарно-технического анализа достигается благодаря использованию методологии контроля качества, что гарантирует выполнение требований. В настоящем стандарте в краткой форме изложено руководство по определению системы метрик для измерения свойств соответствующих характеристик качества.

Настоящий стандарт содержит части, которые используют полностью или частично в своей работе следующий круг лиц:

- разработчики методов расчета (частные лица или организации, осуществляющие деятельность в области разработок, в том числе анализ требований, проектирование и тестирование компонентов) для документального подтверждения актуальности того или иного метода расчета, возможно, для конкретного применения. Часть разработки метода расчета включает в себя определение прецизионности и границ применимости, а также независимое тестирование;

- разработчики методов расчета (частные лица или организации, которые осуществляют поддержку компьютерных моделей, их поставку и оценку качества в рамках обеспечения оценки и контроля качества) для документального оформления процесса разработки программного обеспечения и предоставления пользователям гарантии, что соответствующие методы испытаний соблюдены с целью обеспечения качества прикладных инструментов;

- пользователи методов расчета (лица или организации, которые используют методы расчета для выполнения анализа), которым необходимо удостовериться в том, что они применяют соответствующий метод для конкретного случая и что данный метод обеспечивает достаточную точность при расчете;

- разработчики норм и стандартов для определения соответствия метода расчета сообразно его применению;

- надзорные органы/представители надзорных органов (частные лица или организации, занимающиеся изучением и утверждением применения методов и инструментов оценки), которые несут ответственность за то, что метод расчета используется в рамках определенной области применения и имеет приемлемый уровень точности;

- преподаватели, которые объясняют применение и допустимость данных методов расчета.

Пользователи настоящего стандарта должны иметь соответствующую квалификацию и компетентность в области пожарно-технического анализа и оценки риска. Важно, чтобы пользователи могли определять параметры, в пределах которых могут быть использованы конкретные методики.

1 Область применения

Настоящий стандарт обеспечивает основу для верификации и валидации всех видов методов расчета, используемых в качестве инструментов для пожарно-технического анализа. В нем не представлены конкретные модели пожара, однако настоящий стандарт предназначен для применения в аналитических моделях, алгебраических зависимостях и сложных численных моделях, которые рассмотрены в качестве методов расчета в контексте настоящего стандарта.

Настоящий стандарт включает:

- процесс, позволяющий определить, что соответствующие уравнения и методы расчета реализованы правильно (верификация) и что рассматриваемый метод расчета точно отображает реальность (валидация);

- требования к документации, подтверждающей пригодность научно-технической основы метода расчета;

- требования к данным, на основе которых должны быть проверены прогнозируемые результаты метода расчета;

- руководство по использованию настоящего стандарта разработчиками и/или пользователями методов расчета и лицами, которые занимаются оценкой результатов, полученных с помощью методов расчета.

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты:

ГОСТ 28195 Оценка качества программных средств. Общие положения

ГОСТ Р ИСО/МЭК 17021-1 Оценка соответствия. Требования к органам, проводящим аудит и сертификацию систем менеджмента. Часть 1. Требования

ГОСТ Р ИСО 19011 Руководящие указания по аудиту систем менеджмента

ГОСТ Р ИСО/МЭК 25010 Информационные технологии. Системная и программная инженерия. Требования и оценка качества систем и программного обеспечения (SQuaRE). Модели качества систем и программных продуктов

ГОСТ Р ИСО/МЭК 25040 Информационные технологии. Системная и программная инженерия. Требования и оценка качества систем и программного обеспечения (SQuaRE). Процесс оценки

Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте национального органа Российской Федерации по стандартизации в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.

3 Термины и определения

В настоящем стандарте применены следующие термины с соответствующими определениями:

3.1 точность (accuracy): Степень точности, присущая приближению, измерению и т.д.

3.2 метод расчета (calculation method): Математический метод, используемый для прогнозирования явлений, вызванных пожаром.

Примечание - Методы расчета могут отражать поведение людей, а также объектов или пожара; по типу они могут быть как вероятностными, так и детерминированными и могут быть выражены как алгебраическими формулами, так и в виде сложных компьютерных моделей.

3.3 калибровка (модели) (calibration of a model): Процесс корректировки параметров моделирования в вычислительной модели с целью повышения их соответствия экспериментальным данным.

3.4 компьютерная (компьютеризированная) модель [computer(rized) model]: Исполняемая компьютерная программа, которая реализует концептуальную модель.

3.5 концептуальная модель (conceptual model): Описание, включающее в себя всю информацию, данные математического моделирования и математические уравнения, описывающие представляющую интерес (физическую) систему или процесс.

3.6 значение по умолчанию (default value): Стандартная настройка или состояние, которые использованы программой, если системой или пользователем не задана другая настройка или состояние.

3.7 детерминированная модель (deterministic model): Метод расчета, использующий научно-обоснованные математические выражения для получения одного и того же результата каждый раз, когда расчет осуществляют с одним и тем же набором значений входных данных.

3.8 инженерная оценка (engineering judgment): Процесс, выполняемый специалистом, который обладает соответствующими квалификацией, образованием, опытом и навыками и который уполномочен выполнять, дополнять, принимать или отклонять компоненты количественного анализа.

3.9 ошибка (error): Опознаваемая неточность на определенном этапе или в действии в процессе расчета, не являющаяся следствием недостаточности знаний.

3.10 модель пожара (fire model): Представление системы или процесса, связанного с развитием пожара, включая динамику и воздействие пожара.

3.11 математическая модель (mathematical model): Набор уравнений, описывающих поведение физической системы.

3.12 показатель измерения (measure): Переменная, которой присваивают значение по результатам измерений.

3.13 измерение (measurement): Набор операций с целью определения значения показателя измерения.

3.14 метрика характеристик качества (metric): Количественная или качественная мера относительного достижения желаемой характеристики качества.

3.15 моделирование (modelling): Процесс построения или модификации модели.

3.16 численная модель (numerical model): Численное представление физической модели (пожара).

3.17 физическая модель (physical model): Модель, демонстрирующая воспроизведение пожара в упрощенных физических условиях (например, масштабная модель).

3.18 вероятностная модель (probabilistic model): Модель, которая рассматривает явление в виде серии последовательных событий или состояний, с использованием математических правил для управления переходом от одного события к другому, например от возгорания к установившемуся горению, а также вероятностей, заданных для каждой точки перехода.

3.19 прецизионность (precision): Ошибка в реализации и решении метода расчета, точно отображающая представленное разработчиком концептуальное описание метода расчета.

3.20 анализ чувствительности (sensitivity analysis): Исследование методом расчета степени, в которой изменения в конкретных параметрах воздействуют на результаты, полученные с помощью метода расчета.

3.21 моделирование (simulation): Выполнение или использование метода расчета.

3.22 расчетная модель (simulation model): Модель, рассматривающая динамические соотношения, существование которых предполагается в реальности, как ряд элементарных операций с соответствующими переменными.

3.23 неопределенность (uncertainty): Потенциальная неточность на определенном этапе или в действии в процессе моделирования, вызванная недостаточностью знаний.

3.24 валидация (validation): Процесс определения степени, в которой метод расчета является точным отражением реальности с точки зрения предполагаемого использования метода расчета.

3.25 верификация (verification): Процесс определения того, что реализация метода расчета точно отражает выполненное разработчиком концептуальное описание метода расчета и решение метода расчета.

Примечание - Фундаментальная стратегия верификации вычислительных моделей представляет собой идентификацию, количественную оценку ошибок в расчетной модели и их решение.

4 Документация

4.1 Общие положения

Техническая документация должна быть достаточно подробной, чтобы все результаты расчетов могли быть воспроизведены с установленной достоверностью и прецизионностью квалифицированным(ой) независимым лицом или группой лиц. Подробная документация методов расчета, в том числе компьютерное программное обеспечение, имеет существенное значение для оценки адекватности научно-технической основы методов расчета и точности вычислительных процессов. Кроме того, составленная должным образом документация может помочь в предотвращении некорректного применения методов расчета. Отчеты о любой верификации и валидации конкретного метода расчета должны становиться частью документации. Достоверность метода расчета включает в себя сравнение результатов с данными реальных пожаров или статистических исследований, испытаний и экспериментов и должна быть подтверждена с применением методики обеспечения контроля качества. Это дает показатель или набор показателей измерений, которые следует сравнивать с заранее определенными критериями, чтобы продемонстрировать соблюдение утвержденных требований к качеству.

В состав документации следует включать:

- техническую документацию с пояснением научной основы метода расчета (см. 4.2);

- руководство пользователя в том случае, если метод расчета является компьютерной программой (см. 4.3).

Необходимые требования к технической документации и руководству пользователя представлены в 4.2 и 4.3. Перечень требований достаточно подробный, однако это не исключает использование других форм информации, которые могут помочь пользователю в оценке применимости и пригодности метода расчета.

4.2 Техническая документация

4.2.1 Общие положения

Техническая документация необходима для оценки научной базы метода расчета. Предоставление технической документации метода расчета является задачей разработчиков модели. Необходимо, чтобы техническая документация детально описывала метод расчета и его основу, отражала возможности метода надлежащим образом и предоставляла пользователям информацию, необходимую для правильного применения метода расчета. В случае расчетов путем алгебраических уравнений, полученных по результатам испытаний путем регрессии, или если применены аналитические решения, пользователю следует полагаться на соответствующую документацию стандартов или аналогичного рода материалы, например на научную литературу. Когда разрабатывают стандарты, которые содержат методы расчета для использования в системе пожарной безопасности, источник(и) для применяемых методов расчета, а также техническую документацию в соответствии с 4.2.2-4.2.4 следует предоставлять, где это применимо.

4.2.2 Описание метода расчета

Описание метода расчета должно включать подробную информацию о нижеследующем:

a) цель:

1) определить решаемую задачу или выполняемую функцию,

2) описать результаты метода расчета,

3) включить технико-экономические обоснования и формулировку обоснованности;

b) теория:

1) описать основную концептуальную модель (главное явление), если применимо,

2) описать теоретическую основу явления и физические законы, на которых основан метод расчета, если применимо;

c) реализация теории, если применимо:

1) представить основополагающие уравнения,

2) описать используемые математические методы, процессы и вычислительные алгоритмы и предоставить их источники,

3) определить все допущения, вложенные в логику, с учетом ограничений по входным параметрам, вызванных областью применения метода расчета,

4) обсудить прецизионность (погрешность) результатов, полученных посредством использования основных алгоритмов, и в случае с компьютерными моделями - любую зависимость от конкретных компьютерных возможностей,

5) описать результаты анализа чувствительности;

d) входные данные:

1) описать необходимые входные данные,

2) предоставить информацию об источнике необходимых данных,

3) для компьютерных моделей перечислить все необходимые вспомогательные программы или внешние файлы данных,

4) предоставить информацию об источнике, содержании и использовании библиотек данных для компьютерных моделей.

4.2.3 Описание верификации и валидации метода расчета

Верификация и валидация метода расчета должны быть полностью и подробно описаны и содержать информацию:

a) о результатах любых попыток оценки прогностических возможностей метода расчета в соответствии с разделом 5, что должно быть представлено в количественном выражении;

b) ссылках на уже выполненные обзоры, аналитические испытания, сравнительные испытания, экспериментальную валидацию и проверки кода. Если в случае с компьютерными моделями валидация метода расчета основана на бета-тестировании, в документации должен быть указан профиль лиц, участвовавших в тестировании (например, участвовали ли они в разработке метода расчета или были обычными пользователями; были ли им предоставлены дополнительные инструкции, не доступные потенциальным пользователям конечного продукта, и т.д.);

c) степени, в которой метод расчета соответствует требованиям настоящего стандарта.

Техническая документация должна быть представлена как один документ, такой как руководство, если речь идет о компьютерных моделях. Всякий раз, когда алгебраические уравнения в явном виде используют для решения задачи пожарной безопасности, соответствующая техническая документация может быть приведена из источников, указанных выше.

Методы обеспечения качества следует использовать для определения соответствия программного обеспечения предполагаемым целям. Данный процесс более подробно изложен в 5.6. Он поддерживается путем определения и использования соответствующих методов обеспечения качества для достижения показателя измерения или набора (полученных) показателей измерения, что позволяет масштабировать качество расчетного метода и определяет, является ли метод расчета достаточно точным, чтобы соответствовать требованиям потенциального пользователя. (См., например, требования ГОСТ 28195 и понятие внутренних и внешних метрик характеристик качества и качества программного продукта в использовании, приведенное в серии стандартов ИСО/МЭК "Требования и оценка качества программного обеспечения (SquaRE)").

Цель оценки метода расчета заключается в том, чтобы сравнить качество метода расчета с требованиями к качеству, в которых отражены потребности пользователей, или даже выбрать метод расчета путем сравнения различных методов расчета.

4.2.4 Примеры с решением

Техническая документация должна включать по меньшей мере один пример (или несколько примеров) с решением. Примеры с решением могут потребоваться как для алгебраических уравнений в явной форме, так и для математических моделей. Последние рассмотрены в 4.3.9. Задача примера с решением заключается в том, чтобы продемонстрировать, какие входные данные необходимы и степень их ограничения, а также показать область применения результата(ов) рассматриваемого метода расчета. Примерами необходимых входных данных и их предполагаемой областью применения или ограничений, в пределах которых вычисление прошло валидацию, могут быть геометрия, свойства материалов и граничные условия. Область применения и точность метода расчета должны быть четко определены в документации.

Примечание - Использование метода расчета вне указанных сценариев, определенных посредством валидации, может приводить к значительным ошибкам в реализуемых решениях вопросов безопасности и мерах противопожарной защиты (см. требования к определению области применения, установленной в процессе валидации, в 5.3).

4.3 Руководство пользователя

4.3.1 Общие положения

Руководство пользователя необходимо, только когда речь идет о компьютерных моделях. Руководство пользователя для компьютерной модели должно позволять пользователю понять применение модели и методологию, воспроизводить компьютерную операционную среду и результаты примеров задач, включенные в руководство, изменять входные данные и осуществлять запуск программы для указанных областей значений параметров и предельных значений. Руководство должно быть изложено достаточно четко, чтобы служить в качестве справочного документа для подготовки входных данных и интерпретации результатов. Документация по установке, техническому обслуживанию и программированию может быть включена в руководство пользователя или представлена отдельно. Для установки программы на компьютере необходимо достаточное количество информации. Все формы документации должны включать в себя имя и необходимую информацию для определения конкретной версии метода расчета и определения организации, ответственной за техническую поддержку метода расчета и дальнейшее обслуживание.

В случае с компьютерными моделями руководство пользователя должно предоставлять в полном объеме информацию, необходимую пользователю, для правильного применения компьютерных моделей (см. 4.3.2-4.3.10).

4.3.2 Описание программы

Описание программы представляет собой полное описание:

a) модели;

b) основных выполненных задач обработки данных и используемые методы и процедуры расчетов (блок-схема может быть полезна);

c) знаний и навыков, необходимых для выполнения стандартных запусков программы.

4.3.3 Инструкции по установке и эксплуатации

В инструкциях по установке и эксплуатации должны быть:

a) указана минимально необходимая аппаратная конфигурация;

b) указан(ы) компьютер(ы), на котором(ых) программа была успешно выполнена;

c) указаны используемые языки программирования и операционные системы, а также версия программного обеспечения;

d) предоставлены инструкции по установке программы;

e) определены стандартное время для персонала и время установки, чтобы выполнить стандартный запуск программы;

f) предоставлена информация, необходимая для оценки времени выполнения программы компьютером с помощью действующих компьютерных систем для определенных задач.

4.3.4 Расчеты программы

Расчеты программы должны содержать:

a) описание функции каждой значительной опции, доступной для решения различных задач, а также руководства по выбору этих опций;

b) определение границы области применения (например, ряд сценариев, для которых достоверно или предположительно действует основополагающая теория, или ряд входных данных, для которых был испытан метод расчета);

c) список ограничений программы, включая соответствующие диапазоны данных и поведение программы, в том случае, когда эти диапазоны превышены, а также, когда данная информация должна быть представлена в технической документации.

4.3.5 Описание входных данных

Описание входных данных должно:

a) предоставить имя и описание каждой входной переменной, ее размерных единиц, значений по умолчанию (при их наличии) и источника (если он не находится в широком доступе);

b) описать все особые способы ввода данных;

c) определить ограничения входных данных на основе устойчивости, точности и практичности данных и применимости модели, а также полученные в результате ограничений для выходных данных;

d) описать все значения переменных по умолчанию и процесс присвоения этих переменных значений, определенных пользователем;

e) если возможна обработка последовательных случаев, объяснить условия сохранения данных или их повторной последовательной инициализации.

4.3.6 Файлы внешних данных

Файлы внешних данных включают:

a) описание содержания и организации файлов внешних данных;

b) ссылки на вспомогательные программы, которые создают, изменяют или редактируют эти файлы.

4.3.7 Требования управления системой

В требованиях управления системой следует:

a) подробно описать процедуру, необходимую для установки и запуска программы;

b) перечислить команды управления операционной системой;

c) перечислить подсказки программы и привести область соответствующих ответов;

d) при возможности, описать, каким образом прервать работу программы во время ее выполнения, продолжить или осуществить выход из нее, а также указать статус файлов и данных после прерывания работы.

4.3.8 Выходные данные

Выходные данные должны содержать:

a) описание выходных данных программы и порядок графического изображения данных;

b) руководство по оценке того, достигает ли программа правильного решения, при необходимости.

4.3.9 Примеры задач/примеры с решением

Примеры задач/примеры с решением предоставляют файлы с примерами соответствующих выходных данных, позволяющих пользователю верифицировать правильность работы программы; эти примеры задач должны выполнять большую часть доступных запрограммированных вариантов (для сравнения см. 4.2.4).

4.3.10 Обработка ошибок

На данном этапе необходимо:

a) предоставить список сообщений об ошибках, которые могут быть сгенерированы программой;

b) предоставить список инструкций для соответствующих действий при возникновении сообщений об ошибках;

c) описать поведение программы при нарушении ограничений;

d) описать процедуры восстановления.

5 Методика

5.1 Общие положения

Верификация и валидация метода расчета - это процессы, используемые для определения точности соответствия метода расчета реальному миру с точки зрения предполагаемых целей его применения (валидация) и степени точности, с которой реализация метода расчета отображает представленное разработчиком концептуальное описание и решение (верификация). Верификация - это процесс определения правильности решения уравнений при условии, что используемые уравнения верны. Валидация позволяет убедиться в том, что фактические результаты соответствуют ожидаемым данным.

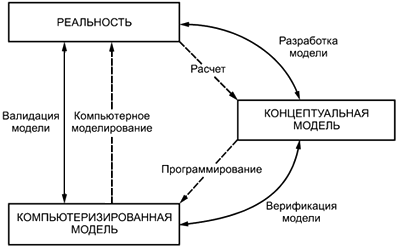
На рисунке 1 в общем схематическом виде представлены этапы моделирования и роль верификации и валидации в этих процессах применительно к компьютерным моделям пожаров.

Рисунок 1 - Пример этапов разработки и оценки компьютерных (компьютеризированных) моделей

Концептуальная модель создается на основе анализа реального мира (иногда физической системы) и состоит из данных математического моделирования и уравнений, описывающих физическую систему (уравнения Навье - Стокса, сохранения энергии и массы, а также дополнительные физические модели, например модели турбулентности, аспекты человеческого поведения, поведение конструкции, риск и т.д.). Верификация рассматривает взаимосвязь между концептуальной моделью и компьютеризированной моделью, в то время как валидация - взаимосвязь между расчетной моделью и реальностью.

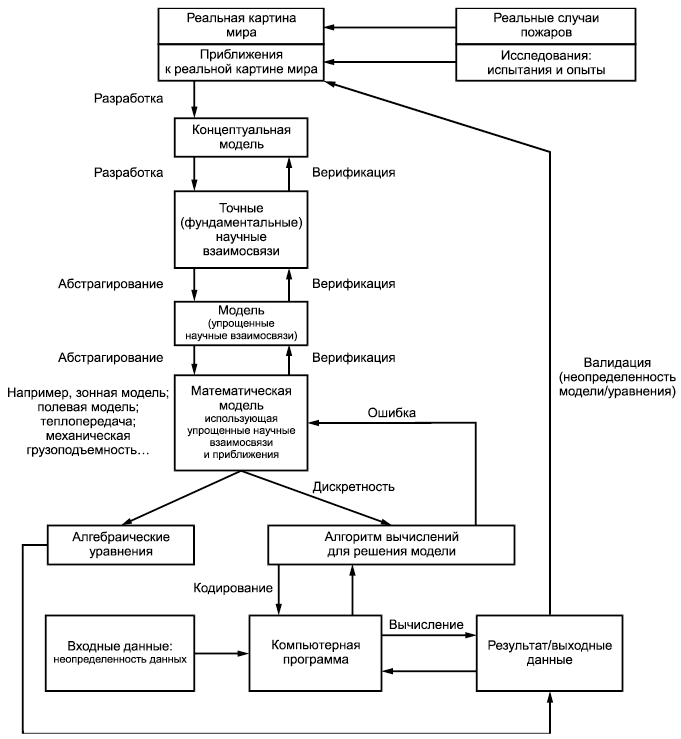
На рисунке 2 более детально раскрыт пример, приведенный на рисунке 1, и представлена блок-схема для широкого применения, которая включает возможные способы использования алгебраических уравнений в случае их целесообразности.

Процедура начинается с получения необходимых знаний об испытаниях и экспериментах или исследованиях для описания явлений реального мира. На основе восприятия реального мира разрабатывают концептуальную модель в виде подробного словесного описания рассматриваемого(ых) процесса(ов), которая в дальнейшем преобразуется в набор математических взаимосвязей. На основе этих взаимосвязей формируется решение (или ряд решений) путем разбиения одной строки за другой - от более сложных уровней до менее сложных, с применением приближений до такой степени, при которой задача может быть решена с достаточной точностью и приемлемым уровнем затрат на решение (например, временные и связанные с производительностью компьютера).

Теоретическая основа метода расчета компьютерной модели должна быть исследована одним или несколькими экспертами, хорошо знакомыми как с научными основами явлений пожаров, так и с техникой расчетов, но не принимавшими участие в разработке модели. Данное исследование должно включать оценку полноты документации, в частности в отношении численных аппроксимаций. Эксперт должен быть способен оценить, достаточно ли существует научных доказательств в научной литературе для использования применяемых подходов. Данные, используемые в программе для постоянных величин и значений по умолчанию, также должны оценивать на предмет точности и применимости с точки зрения метода расчета и предполагаемого использования. Последнее требование особенно важно в тех случаях, когда данные, используемые для численных постоянных, могут иметь специальные значения для конкретных сценариев. Практические верхние и нижние предельные значения переменных, используемых в качестве входных данных, должны быть четко определены, чтобы ограничить их применение проверенной областью.

Рисунок 2 - Схематическое изображение валидации и верификации модели

Между этапами преобразования элементов в систему, пригодную для дальнейшей работы, необходимо выполнять процессы верификации и валидации с целью постоянной проверки системы на возможные источники ошибок. В связи со сложностью математической интерпретации явлений пожара в примере на рисунке 2 приведены подробные данные, которые не нужны для оценки (эмпирических) методов расчета, т.е. алгебраические уравнения, которые также рассмотрены в настоящем стандарте и представлены в определенной ячейке таблицы.

Методология не ограничена расчетом распространения пожара и подобными задачами, но может быть применена относительно валидации и верификации методов расчета поведения и движения людей, поведения конструкции и оценки рисков.

5.2 Верификация

Верификация представляет собой процесс определения того, что реализация метода расчета в точности соответствует его концептуальному описанию и решению, предоставленным разработчиком. Это не подразумевает, что разрешающие уравнения являются пригодными, однако означает, что уравнения реализованы и решены правильно и их реализация точно соответствует концептуальному описанию метода расчета и его решению, предоставленным разработчиком метода.

Таким образом, цель процесса верификации заключается в том, чтобы проверить правильность программного кода и оценить контроль численных ошибок, которые могут быть разделены на три категории: округление, усечение и дискретизация. Ошибки округления возникают вследствие того, что компьютеры предоставляют действительные числа, используя конечное число цифр. Ошибки усечения возникают при замене непрерывного процесса конечным. Например, такие ошибки могут происходить, когда бесконечный ряд усекается после конечного числа членов или когда повторное действие прекращается после того, как критерий сходимости был удовлетворен. Ошибки дискретизации возникают, когда непрерывный процесс, такой как вычисление производной, аппроксимируется дискретным аналогом, таким как разделенная разность. Верификация вычислительного метода должна включать в себя анализ и обсуждение используемых методов и присущих ограничений в конкретных выбранных вариантах.

5.2.1 Проверка компьютерных программ

Программный код может быть проверен на структурной основе, вручную или с помощью программ проверки кода, с целью выявления нарушений и несоответствий в компьютерном коде. Обеспечение четкого определения и регистрации методов и методологий, используемых для проверки программного кода, а также любых обнаруженных недостатков повышает уровень уверенности в способности программы надежно обрабатывать данные, однако это не может служить показателем возможной пригодности и точности используемой программы. Не всегда ошибка указывает на непригодность программы, однако документирование этих "ошибок" предотвращает использование ошибочных режимов программы.

5.2.2 Временная и пространственная дискретизация

Математические модели, как правило, выражены в виде дифференциальных или интегральных уравнений. Модели, в целом, имеют сложную структуру, и аналитические решения часто бывает трудно найти. Для нахождения приближенных решений необходимы численные методы. В численном методе происходит дискретизация непрерывной математической модели, то есть приближение с помощью дискретной, численной модели. Дискретизация осуществляется во времени и в пространстве (разбиение на сетки).

Непрерывная математическая модель может быть дискретизирована множеством различных способов, в результате чего будет получено множество различных дискретных моделей. Для достижения хорошего приближения к решению непрерывных моделей дискретная модель должна имитировать свойства и поведение непрерывной модели. Это означает, что дискретное решение должно сходиться к решению (если оно существует) непрерывной задачи при уменьшении параметров дискретизации (временного шага, пространственной сетки и т.д.). Это достигается путем выполнения требований совместимости и устойчивости. Совместимость означает, что дискретная модель максимально приближена к непрерывной модели в отношении некоторых оценок, например норм определенных величин. Устойчивость означает, что погрешность не увеличивается по мере выполнения программы.

Следует выявлять и изучать формальный порядок ошибки в пространственной и временной дискретизации. Возможно, не удастся провести исчерпывающий анализ, однако необходимо осуществить как часть процесса верификации анализ представления уравнений в дискретную числовую форму.

Многие задачи, связанные с пожаром, включают взаимодействие различных физических процессов, таких как химические или тепловые процессы и механические реакции. Временные и пространственные масштабы, относящиеся к этим процессам, могут существенно отличаться, что приводит к возникновению численных трудностей. Следовательно, при решении дифференциальных уравнений необходимо позаботиться о выборе нужных временных и пространственных шагов, чтобы обеспечить устойчивость (особенно в отношении временного шага для переходных вычислений) и достаточную сходимость вычислений. Некоторые численные методы могут быть использованы для динамического мониторинга параметров дискретизации в соответствии с требованиями устойчивости и точности (например, в отношении пространственной дискретизации, апостериорная оценка ошибок, объединенная с динамическим измельчением сетки). Рекомендуется использовать такие методы, особенно для временной устойчивости, а также для нелинейных задач, которые встречаются в зонных моделях. В этом случае документация программы должна в полной мере объяснять, каким образом это было достигнуто, и должны быть представлены численные эксперименты со ссылкой на достоверность используемого алгоритма. Это не мешает пользователю проводить для некоторых расчетов исследование сходимости времени и пространства. Каким образом выполняется данная задача систематически в случае выбора параметров дискретизации, остается на усмотрение пользователя.

5.2.3 Проверки сходимости итераций и устойчивости

Важно, чтобы реализация концептуальной модели в виде компьютерной программы была выполнена правильно. Для этого необходимо осуществить следующие действия, когда это применимо:

a) проверить критерии остаточных ошибок;

b) проверить устойчивость выходных переменных;

c) применить глобальные проверки по сохранению соответствующих величин;

d) по мере возможности, проводить сравнение с аналитическими решениями;

e) проводить сравнение с более точными решениями, полученными с помощью более полных моделей, которые достоверно прошли верификацию и валидацию;

f) проверить воздействие искусственных граничных условий для незамкнутых задач.

5.2.4 Обзор числовой обработки моделей

Важная часть верификации модели заключается в том, чтобы удостовериться, что уравнения и методы, указанные в документации, описывающей подход, были реализованы надлежащим образом, что подразумевает оценку документации, реализацию уравнений в компьютерном коде и анализ используемых методов дискретизации и численных методов.

5.3 Валидация

5.3.1 Общие положения

В данном пункте представлены процедуры с целью определения точности метода расчета для широкого спектра применений. Строгое соблюдение процедуры валидации необходимо, чтобы установить диапазон применения метода расчета и определить точность метода расчета в приемлемом диапазоне. Это является верным для любого вида метода расчета, представленного в настоящем стандарте. Корреляции - это допустимые прогнозирующие инструменты, которые должны быть проверены таким же образом, как компьютерные модели с использованием аналогичных методов.

Даже для простейших случаев задач по оценке пожаров не существует универсальных аналитических решений, то есть решений в аналитическом виде. Однако существует возможность выполнить два типа проверки. Первый тип представляет собой способ, с помощью которого отдельные алгоритмы сверяют с алгоритмами в экспериментальной работе. Второй тип состоит из простых экспериментов, например теплопроводность и излучение, результаты в которых асимптотичны. В частности, в простом испытании с одним помещением при отсутствии возгорания температура должна асимптотически приходить в равновесие к единому значению. Модель должна быть в состоянии воспроизвести это поведение. Наконец, есть возможность вычислить решения для ситуаций, в которых существуют аналитические ответы, однако такие ситуации можно воспроизводить в эксперименте, но не естественным путем.

Расхождение при сравнении алгебраического уравнения или компьютерной модели с экспериментальными данными связано со степенью неопределенности, в которой метод расчета является точным отражением реальной картины с точки зрения его предполагаемого использования (валидация), а также с погрешностью в концептуальном описании метода расчета, предоставленном разработчиком, и решением метода расчета (верификация).

В настоящем стандарте предусмотрены две процедуры, любая из которых может сопровождаться валидацией, которую проводит заинтересованная сторона. Эти процедуры называются "слепая" и "открытая" валидация.

При проведении процедуры слепой валидации сторона, которая проводит валидацию, имеет данные только начальных и граничных условий эксперимента, необходимых для выполнения методов расчета, проходящего валидацию. Эти данные могут включать любой параметр (например, скорость выделения тепла), для которого прогнозирующую способность модели не проверяют. Сторона, проводящая валидацию, не имеет доступа к экспериментальным измерениям выходных данных метода расчета, проходящего валидацию.

В открытой процедуре сторона, проводящая валидацию, имеет данные о начальных и граничных условиях эксперимента, а также сведения об измерениях выходных параметров метода расчета, проходящего валидацию, до того, как выполняется метод расчета. В литературе встречаются и другие определения, используемые по данному вопросу, такие как "априори", "апостериори", "абсолютно слепая" и "наполовину слепая" валидация. В настоящем стандарте приняты и использованы только два термина, "слепая" и "открытая" валидация, как определено выше, которые охватывают диапазон условий, возникающих в процессе валидации.

Существует ряд достоинств и недостатков этих двух процессов валидации. Заинтересованная сторона должна самостоятельно определить, какой из процессов валидации больше соответствует ее потребностям. Пользователь настоящего стандарта должен соблюдать его требования, проводя открытую или слепую валидацию.

Процедура, которую должны использовать в процессе открытой или слепой валидации, представлена в 5.3.2 и 5.3.3.

Во всех случаях обеих процедур валидации необходимо определять сравнительные метрики характеристик качества.

Далее должен быть выбран характер значений, подлежащих сравнению. Если модель прошла валидацию для общей скорости выделения тепла, это не означает ее прохождение валидации для других параметров. Ряд взаимосвязанных типов поведения моделей может приводить к соответствию с общей кривой выделения тепла, однако это происходит при неправильном рассмотрении предметов горения, которые выделяют тепло.

Зонная модель в первую очередь решает глобальные балансы массы и энергии по слоям.

Первым шагом в процессе валидации для таких моделей является проверка скорости выделения тепла и массы, затем могут быть сделаны сравнения значений, связанных с каждым слоем, такие как граница слоя, температура и состав.

С точки зрения модели вычислительной гидродинамики CFD должны быть подтверждены глобальная валидация и локальная валидация энергии, массы, массы по видам и величин перемещения. Полная валидация модели потребует глобальных данных, таких как общая потеря массы или выделение тепла HRR, и локальных данных, таких как скорость движения воздушной массы, местный состав газа и местные значения температур.

5.3.2 Процедура открытой валидации

Не существует строгих требований к проведению аудита процедуры открытой валидации. Процедура, которую следует соблюдать в процессе открытой валидации, представлена ниже:

a) сторона, проводящая валидацию, имеет или получает доступ к начальным и граничным условиям экспериментов, а также к измерениям выходных параметров, прогнозируемых с помощью их метода расчета, прежде чем осуществляют методы расчета;

b) граничные условия и входные значения, которые будут использованы для методов расчета, должны быть установлены и задокументированы прежде, чем будут осуществлены методы расчета;

c) методы расчета ни в коем случае не следует осуществлять повторно с измененными граничными условиями экспериментов в качестве входных значений, за исключением рамок анализа неопределенности при оценке риска, где рассматривается результат неопределенности в экспериментальных данных.

5.3.3 Процедура слепой валидации

Процедура слепой валидации требует проведения аудита для того, чтобы подтвердить выполнение процедур, приведенных в данном пункте. Аудит можно проводить либо в соответствии с требованиями, установленными организацией, осуществляющей проверку, либо более формально согласно ГОСТ Р ИСО 19011 и ГОСТ Р ИСО/МЭК 17021-1 в качестве аудита, проводимого "первой" или "второй стороной", либо "аудита и сертификации, проводимых третьей стороной".

Процедура процесса слепой валидации заключается в следующем:

a) сторона, проводящая валидацию, должна иметь данные только о начальных и граничных условиях эксперимента, которые необходимы для осуществления методов расчета, проходящих валидацию. Сторона, проводящая валидацию, не должна иметь доступ к результатам экспериментальных измерений данного метода расчета, который проходит валидацию;

b) процесс слепой валидации может быть использован только тогда, когда должны быть проведены новые эксперименты по валидации или когда существуют опыты валидации, не доступные для общественности и для стороны, проводящей валидацию;

c) спецификация экспериментов, используемая для процесса валидации, включая начальные и граничные условия, должна быть достаточно подробной, чтобы обеспечить аналитиков методов расчета всеми необходимыми входными данными;

d) в зависимости от цели валидации в качестве граничного условия и вводных данных для метода расчета могут использовать некоторые параметры, такие как скорость выделения тепла, которые должны быть определены при осуществлении валидации;

e) сторона, проводящая валидацию, должна иметь доступ к экспериментальным измерениям, соответствующим выходным данным расчета, проходящего валидацию, после того, как метод расчета был осуществлен и результаты были предоставлены аудитору;

f) эксперименты, в ходе которых получают результаты, используемые для валидации метода расчета, могут проводить либо до, либо после осуществления методов расчета;

g) в некоторых случаях начальные и граничные условия экспериментов, предоставляемые стороне, проводящей валидацию, должны быть изменены после того, как эксперименты были проведены, чтобы отразить их фактические условия. В таких случаях пересмотренные граничные условия должны быть предоставлены стороне, проводящей валидацию, для повторного осуществления расчетных методов, если расчеты были осуществлены до проведения опытов;

h) во всех случаях должно быть достигнуто соглашение о граничных условиях и входных данных, используемых для методов расчета, до окончательного осуществления расчетных методов и до выхода экспериментальных измерений выходных данных расчета, проходящего валидацию;

i) метод расчета ни в коем случае не может быть повторно осуществлен после того, как были получены экспериментальные измерения выходных данных расчета, проходящего валидацию;

j) результаты метода расчета, подвергаемого валидации, должны быть предоставлены аудитору до того, как будут получены экспериментальные измерения выходных данных расчета;

k) сторона, проводящая валидацию, должна разработать специальную процедуру валидации в соответствии с настоящим стандартом. Данная процедура должна быть утверждена аудитором до начала процесса валидации.

5.3.4 Отчетность по валидации

Результаты процесса открытой и слепой валидации должны быть документально оформлены и включать в себя следующее:

a) описание экспериментов и измерений, включая неопределенность в измерениях (см. приложение В);

b) входные данные, используемые для методов расчета;

c) сравнение результатов метода расчета с экспериментальными данными с использованием установленных метрик характеристик качества в количественном выражении;

d) представление расхождений в виде таблиц с использованием установленных метрик характеристик качества в количественном выражении.

Примечание - Расхождение может быть связано с ошибкой и неопределенностью в методе расчета;

e) граничные и начальные условия экспериментов и, следовательно, сценарии пожаров, для которых применима валидация.

5.3.5 Особые соображения в сравнении прогнозов с данными

Поскольку результаты алгебраической формулы в большинстве своем представляют точечные прогнозы, для них применимы те же принципы, что и для точечных прогнозов компьютерных моделей. Точечные прогнозы следует соотносить с данными (экспериментов, исследований) каждый раз, когда они доступны для рассматриваемой задачи и если они были получены с эквивалентным набором начальных и граничных условий.

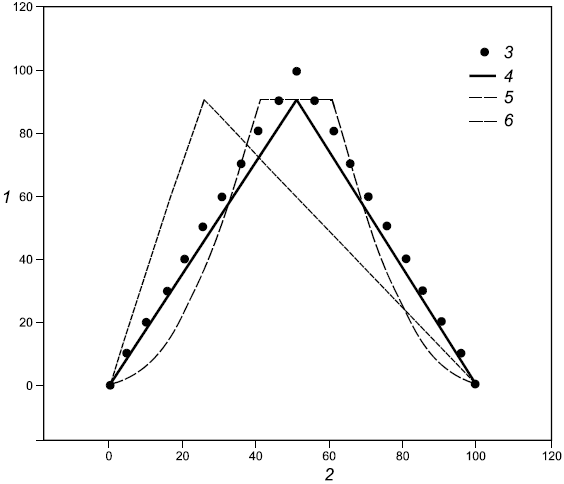
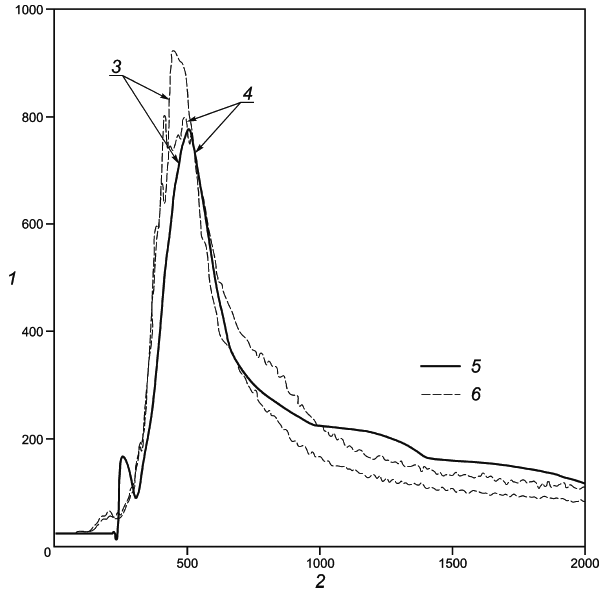
Для сравнения прогнозирования временной величины с данными в приложении В представлены два метода для количественной оценки сходства и различия двух кривых, таких как изменение во времени температуры верхнего слоя для прогнозирования модели и эксперимента. Первый метод реализован путем рассмотрения кривых как бесконечномерных векторов и дальнейшего описания различий с помощью векторного анализа. Данный анализ обеспечивает количественный метод валидации моделей пожара и количественной оценки неопределенности в опытных данных.

Второй метод, называемый нормированным евклидовым расстоянием, рассматривает различия между результатами расчетов и измерениями в течение всего пожара. Данная метрика обеспечивает информацию о глобальных ошибках и дает полный обзор возможностей программного кода.

В приложении В показано применение обоих методов.

5.4 Обзор теоретической и экспериментальной основы вероятностных моделей

Уравнения, используемые в вероятностной модели как часть оценки риска, - это, как правило, уравнения, определяющие риск с точки зрения вероятностной функции в пространстве, установленном сценариями, и уравнения, используемые для получения необходимых вероятностей из других более доступных вероятностей. Исследование правильности уравнений должно дать ответы на следующие вопросы:

a) Использует ли модель только четко определенные вероятностные переменные и параметры?

Вероятностное моделирование и оценка риска, как правило, используют экспериментальные базы данных или инженерные оценки для получения переменных и параметров вероятности. Доказательство точности оценки переменной или параметра с одним значением может быть получено путем сравнения с альтернативными оценками, рассчитанными таким же способом на основе независимых данных. Например, значения оценки, предоставленные одной группой экспертов, могут сравнивать со значениями оценки, полученными от другой группы экспертов. В таком случае особое внимание следует уделять характеристикам тех специалистов, которые с наибольшей вероятностью повлияют на оценку. Кроме того, вероятность на основании опыта (например, вероятность возгорания) может быть верифицирована путем сравнения с подобными примерами вероятности на основании опыта, полученного в другом месте или в другое время.

Выходные переменные оценки риска, как правило, основаны на вероятности и последствиях, где последние являются производными детерминированной модели. Прогнозы детерминированной модели могут быть подтверждены в порядке, описанном в настоящем стандарте. Комбинированный расчет риска либо для всего расчета, либо для подсистемы, либо другой части расчета может быть подтвержден путем сравнения с фактическим ущербом. В тех случаях, когда вероятностные значения основаны на опыте, значение ущерба, используемое для валидации, должно быть получено в тех же местах и в тот же период времени, которые использовались для определения значений вероятности.

b) Следуют ли вероятностные переменные, параметры и расчеты законам вероятностей (например, вероятности должны находиться в пределах от 0 до 1)?

c) Являются ли все уравнения, использующие условные вероятности, полными? Например, для уравнения . Если опустить вторую часть выражения, то необходим конкретный случай, при котором либо P (не B), либо, что чаще встречается, P (A задано не B)

равно нулю или приблизительно равно нулю.

d) Явно ли выражено определение риска, связывая его меру с вероятностью и последствиями сценариев? Если нет, то существует ли подразумеваемое выражение?

e) Охватывает ли выражение, определяющее риск с точки зрения сценариев, все возможные сценарии? Если нет, то всесторонне ли в расчете учтено воздействие пропущенных сценариев на расчет?

f) Затрагиваются ли в расчете непосредственно неопределенности, связанные с вероятностными переменными и параметрами? Рассматриваются ли и учитываются ли случайные неопределенности и источники систематических ошибок?

g) Если какие-либо уравнения упрощаются, сравниваются ли они с точки зрения точности с их аналогами в полном виде?

5.5 Анализ чувствительности

Анализ чувствительности метода расчета представляет собой исследование степени воздействия изменений в конкретных параметрах на результаты, полученные с помощью метода расчета. Прогнозы могут быть чувствительны к неопределенностям в исходных данных, к уровню строгости, принятому в моделировании соответствующих физических и химических явлений, и к применению неадекватных числовых операций.

Правильно спланированный и проведенный анализ чувствительности позволяет:

a) определить доминирующие переменные в методах расчета;

b) определить допустимую область значений для каждой входной переменной;

c) продемонстрировать чувствительность выходных переменных к изменениям во входных данных;

d) информировать и предупреждать потенциальных пользователей о степени и уровне тщательности, необходимых при выборе входных данных и запуске модели;

e) предоставить информацию о том, какие параметры следует отслеживать в крупномасштабных испытаниях.

Проведение анализа чувствительности сложной пожарной модели является трудной задачей. Многие модели требуют широкий набор входных данных и генерируют прогнозы для многочисленных выходных переменных в течение моделируемого промежутка времени. Выбранный метод для использования зависит от целей исследования, требуемых результатов, имеющихся ресурсов и сложности анализируемой модели. Методы, доступные для проведения анализа чувствительности, приведены в приложении С.

5.6 Обеспечение качества

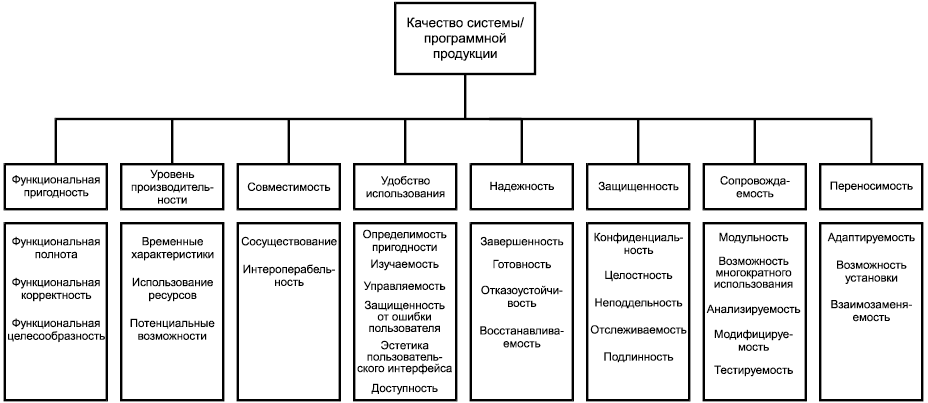
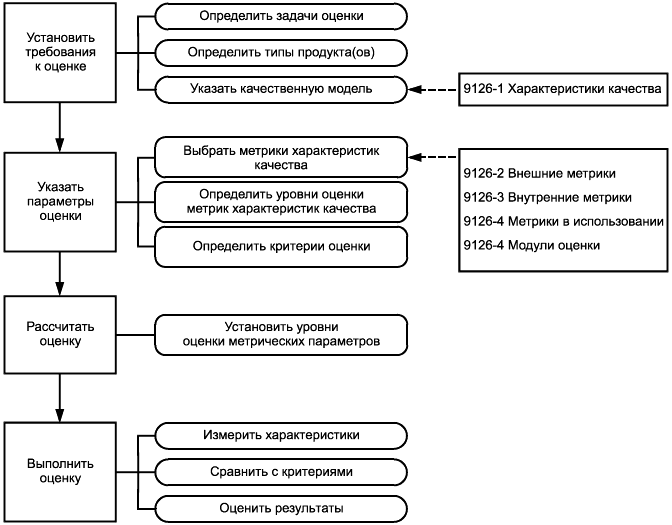
Рекомендуется проводить оценку компьютерных программ с целью обеспечения оценки качества. Качество таких программ можно оценить с помощью специальных моделей. Они используют процедуры, способствующие оценке как "внешнего качества", важного для конечного пользователя, так и "внутреннего качества", необходимого для надлежащего функционирования программы. Показатели качества программного обеспечения делятся на восемь характеристик (функциональная пригодность, уровень производительности, совместимость, удобство использования, надежность, защищенность, сопровождаемость и переносимость), которые, в свою очередь, подразделяются на подхарактеристики (см. рисунок 3). Для каждой характеристики и подхарактеристики качество программного обеспечения следует определять набором измеренных внутренних показателей. Характеристики и подхарактеристики должны быть измерены внешне в такой степени, в которой позволяет система, содержащая данное программное обеспечение. Важным элементом обеспечения качества в методах расчета пожарной безопасности является определение пригодности и точности методов (функциональная пригодность).

Рисунок 3 - Модель внешнего и внутреннего качества, показывающая характеристики и подхарактеристики

Для валидации методов расчета пожара необходимо предъявлять строгие требования контроля качества ввиду того, что они находятся в зачаточной стадии разработки и при этом широко применяются в области пожарно-технического анализа. Развитие пожара представляет собой сложное явление, оно охватывает очень широкий спектр сценариев и включает в себя множество факторов, которые могут на него повлиять. Одним из наиболее важных элементов обеспечения качества метода пожарного расчета является определение диапазона валидации и, следовательно, применимости, т.е. для каких конкретных сценариев пожара был утвержден метод расчета. Адекватная процедура валидации, как описано в 5.3, для определения точности метода расчета пригодных метрик и выявления диапазона применимости - ключ к обеспечению качества. Использование правильной точности методов пожарного расчета для определения факторов безопасности, необходимых в более широком контексте применения пожарно-технического анализа пожарной безопасности, в соответствии с требованиями [16], - конечная цель обеспечения принятия решений о качестве в целях пожарной безопасности.

Для оценки качества метода расчета применяют процедуры, приведенные в ГОСТ 28195 и серии нормативных документов на основе ГОСТ Р ИСО/МЭК 25010 и ГОСТ Р ИСО/МЭК 25040. Сокращенная версия процедуры согласно ГОСТ 28195 приведена в приложении D.

6 Требования к справочным данным для валидации метода расчета

6.1 Общие положения

Справочные данные для валидации метода расчета могут быть получены в ходе экспериментов, одного или нескольких аналогичных исследований подробно документированных случаев пожара либо других проверенных методов расчета в соответствии с параметрами и другими величинами, которые подлежат валидации.

Данные, используемые при определении, установке или оценке величины в методе расчета, не могут применять для валидации этой величины. Для процедуры валидации необходимо использовать независимые данные.

Различия между величиной метода расчета и данными, используемыми в ней для валидации, могут быть связаны с наличием ошибок в этой величине или в данных.

Для обоснования выводов о применимости метода расчета необходимо, чтобы при выполнении валидации оценивались величина, характер ошибок в справочных данных и влияние этих ошибок на различия между расчетными величинами и данными. Таким образом, необходимо, чтобы полноту, качество, прецизионность (погрешность) справочных данных можно было охарактеризовать одним из следующих пунктов, прежде чем они могут быть использованы для валидации.

Для экспериментальных данных необходимо проводить оценку повторяемости и воспроизводимости процедуры испытания, являющейся источником данных. Характеристики прецизионности и погрешности исходных данных могут быть получены из доступных характеристик аппарата или устройства измерения, использованного для получения данных.

Для (статистических) данных исследований необходима оценка репрезентативности плана исследования и полученной выборки. Кроме того, следует выявить неопределенность, связанную с размером выборки.

Для данных расследования пожара необходимо указать, каким образом были получены эти данные.

Для данных из других проверенных методов расчета необходимо свидетельство о валидации этих методов наряду с характеристикой их прецизионности (погрешности), источников и величин ошибки.

Необходимо провести оценку соответствия условий сбора справочных данных условиям, предполагаемым в методе расчета. Это включает в себя начальные и граничные условия. К примеру, если в экспериментах использованы справочные данные об осуществлении эвакуации населения, состоящего исключительно из молодых, здоровых взрослых людей, то этих данных недостаточно для валидации метода расчета, применяемого к смешанным группам населения.

Необходимо в полном объеме проверить метод расчета, а также отдельно - его подсистемы и подмодели. Соответствующие данные должны быть определены и получены для каждого из этих уровней валидации.

Следует оценить все процедуры сокращения, преобразования или интерпретации применительно к необработанным данным с целью получения справочных данных, пригодных для использования в процессе валидации. Например, если необработанные данные исследования доступны только для выбранных высотных офисных зданий в одном городе, то его применимость к другим типам зданий, другой высоты, в других городах и других странах является неопределенной. Необходимо отмечать и оценивать такое неполное соответствие.

Следует оценить независимость формирования справочных данных от разработки метода расчета.

Полная валидация метода расчета требует оценки полного спектра выходных данных для полного перечня случаев и условий. Справочные данные требуются для проведения наиболее полной оценки, по мере возможности, и необходимо, чтобы любые ограничения на диапазон выходных данных и оцениваемых случаев были явно указаны, по возможности в форме ограничений по применению метода расчета, для которого валидация была успешно завершена. Например, если экспериментальные данные доступны только для значений температуры на уровне потолка, то для температурных прогнозов метода расчета в других местах в помещении валидация не является непосредственно пройденной.

6.2 Особые требования к данным для валидации

Первым шагом является сравнение прогнозов модели или аналитического метода с соответствующими данными. Как было отмечено во введении, в то время как модель является реализацией теоретической концепции, экспериментальные данные становятся представлением о реальном мире. В этом контексте важно убедиться в том, что соответствующие модели и входные данные отражают практический опыт. Оба представления имеют ограничения и присущие им ошибки, и соответствующие неопределенности в них должны быть включены в сравнение. С точки зрения валидации корректность заключается в том, что модель дает соответствующие ответы на входные данные, которые представлены в рассматриваемых сценариях. Процесс валидации включает в себя сообщение о диапазоне действительности входных данных.

Эти данные, как правило, включают в себя:

- обеспечение полноты данных об окружающей среде (например, перепады температуры в зданиях или разницу температур внутри и снаружи здания, воздействие ветра);

- использование точных данных о свойствах; если используют постоянные значения, анализ чувствительности должен показать их влияние на выходные данные; если постоянные значения используют вместо, например, температурно-зависимых переменных, то исход этого приближения (см. выше) следует оценивать в диапазоне применимости модели или метода расчета.

Данные, заимствованные из литературных источников, должны быть снабжены ссылками на них. Литературными источниками могут быть справочники, стандарты, журналы и научные доклады. В тех случаях, когда данные из рецензируемых источников не доступны, эти данные должны быть проверены в сравнении с подтвержденными данными.

Те же принципы применяют к реальным явлениям, независимо от степени сложности их представления с помощью расчетных методов или моделей. Они могут быть использованы для прогнозирования развития пожара в здании, или процессов эвакуации, или того и другого, в то время как аспекты человеческого поведения также могут влиять на результаты и должны оцениваться на основе тех же принципов.

Приложение A
(справочное)

Неопределенность

A.1 Неопределенность измерения данных

A.1.1 Общие положения

В подразделе A.1 приведена информация с целью содействия лицам, проводящим эксперименты, в выражении неопределенности результатов их измерений, а также пользователям модели в оценке полезности экспериментальных данных при выполнении эмпирической валидации модели. Не все опубликованные экспериментальные данные содержат информацию о неопределенности данных.

В целом результат измерения - это только результат приближения или оценки определенной величины, подлежащей измерению, и, таким образом, результат является полным только в сопровождении количественного суждения о неопределенности. Неопределенность результата измерения, как правило, состоит из нескольких компонентов, которые в подходе, используемом Международным советом по мерам и весам, могут быть сгруппированы в две категории в зависимости от метода, используемого для оценки их численных значений:

- категория A - те компоненты, которые оценивают путем статистических методов;

- категория B - те компоненты, которые оценивают посредством других средств.

Неопределенность, как правило, делят на две составляющие: случайную и систематическую. Каждый компонент, вносящий вклад в неопределенность измерения представлен в виде предполагаемого стандартного отклонения, которое называется стандартной неопределенностью, обозначается символом , и равен положительному квадратному корню из расчетной дисперсии . Компонент неопределенности в категории А может быть представлен в виде статистически рассчитанного стандартного отклонения , равного положительному квадратному корню из статистической оценки дисперсии и связанного с числом степеней свободы . Для такого компонента стандартная неопределенность . Аналогичным образом, компонент неопределенности в категории B представлен величиной , которую могут рассматривать как приближение к соответствующему стандартному отклонению; он равен положительному квадратному корню из , который может быть рассмотрен как приближение к соответствующей дисперсии и получен из предполагаемого распределения вероятностей, основанного на всем объеме имеющейся информации. Поскольку величина рассмотрена как дисперсия, а - в качестве стандартного отклонения для такого компонента, стандартная неопределенность просто представлена .

A.1.2 Оценка стандартной неопределенности категории A

Оценка стандартной неопределенности категории A может быть основана на любом допустимом статистическом методе обработки данных.

Примером является вычисление стандартного отклонения среднего значения ряда независимых наблюдений с помощью метода наименьших квадратов, чтобы привести кривую в соответствие с данными для оценки параметров кривой и их стандартных отклонений.

Данный отчет не является попыткой предоставить подробные статистические методы проведения статистической оценки.

A.1.3 Оценка стандартной неопределенности категории B

Оценка неопределенности категории B, как правило, основана на научной оценке с использованием всей необходимой доступной информации, которая может включать:

a) данные предыдущих измерений;

b) опыт или общие знания работы и свойств соответствующих материалов и инструментов;

c) спецификации производителя;

d) данные, представленные в калибровочном отчете и других отчетах, а также неопределенности по материалам справочников.

Поскольку надежность оценки компонентов неопределенности зависит от качества имеющейся информации, рекомендуется обеспечить, чтобы все параметры, от которых зависит измерение, максимально варьировались, чтобы оценка в наибольшей степени основывалась на данных наблюдений.

При возможности, использование эмпирических моделей процесса измерения на основе долгосрочных количественных данных, а также контрольных стандартов и контрольных карт, которые могут подтверждать, что процесс измерения находится под статистическим контролем, должны быть составной частью отчета для получения потенциально надежной оценки компонентов неопределенности.

A.1.4 Суммарная стандартная неопределенность

Суммарную стандартную неопределенность измеренного результата, обозначаемую символом , используют для обозначения стандартного отклонения результата. Она может быть получена путем объединения отдельных стандартных неопределенностей , полученных в результате оценки категории А или В с использованием обычного метода для объединения стандартных отклонений. Данный метод часто называют "закон распространения неопределенности" или "метод квадратного корня из суммы квадратов". Суммарная стандартная неопределенность является широко используемым показателем измерения неопределенности.

A.1.5 Расширенная неопределенность

Хотя суммарную стандартную неопределенность используют для выражения неопределенности многих результатов измерений, часто требуется показатель измерения, определяющий интервал в результате измерения, , в котором значение измерения может с уверенностью считать ложным. Этот показатель измерения известен как расширенная неопределенность, обозначаемая символом , которая может быть получена путем умножения на коэффициент охвата, обозначаемый . Следовательно, , и можно с уверенностью утверждать, что и часто записывается в виде .

В целом коэффициент охвата может быть выбран с желаемым уровнем уверенности. Как правило, находится в промежутке от 2 до 3. Когда применяют нормальное распределение и имеет незначительную неопределенность, присвоение значения 2 определяет интервал, имеющий уровень уверенности, приблизительно равный 95%, а присвоение значения 3 - уровень уверенности, составляющий более 99%. В текущей международной практике используют значение , равное 2.

A.1.6 Предоставление данных неопределенности

Для того чтобы сообщить о неопределенности измерений, нужно предоставить значение совместно с коэффициентом охвата , используемым для его вычисления, или сообщить значение . При предоставлении результата измерения и его неопределенности следует вносить в отчет следующую информацию:

- список всех компонентов стандартной неопределенности вместе с их степенью свободы, где это применимо, и полученные в результате значения ; компоненты должны быть определены в соответствии с методом, используемым для оценки их численных значений (статистических или других средних значений);

- подробное описание процесса оценки каждого компонента стандартной неопределенности,

или добавить ссылки на опубликованный документ.

Приложение B
(справочное)

Примеры методов валидации

B.1 Общие положения

Ключевое значение для валидации моделей пожара имеет возможность количественно определить различие между прогнозами модели и экспериментальными измерениями, или между двумя прогнозами модели, или двумя наборами экспериментальных данных. Эти методы считаются пригодными для сравнения моделей с экспериментами, сравнения моделей между собой и сопоставления прогнозов модели с данными датчиков для использования при обнаружении и прогнозировании пожаров в системах реального времени.

B.2 Метод функционального анализа

Первый метод валидации, представленный в настоящем приложении, использует математический метод, известный как функциональный анализ. Функциональный анализ представляет собой сочетание методов линейной алгебры, анализа и геометрии. Эта область исследования, впервые появившаяся в 1900 г. в работе Гильберта и др., приобретает все большее значение в ряде областей, включая теоретическую физику, экономику и технические науки. Функциональный анализ играет важную роль для ответов на вопросы по дифференциальным уравнениям, численным методам, теории приближений и прикладным математическим методам. Задачи приведены в векторном представлении, и соответствующие операции над векторами могут быть выполнены, чтобы провести количественный анализ свойств лежащей в основе физической системы. Основными операциями над векторами, представляющими интерес, являются норма, мера длины вектора и скалярное произведение, а также мера угла между двумя векторами.

Для того чтобы выполнить общее сравнение двух кривых, данное сравнение по одной общей точке может быть расширено до нескольких точек. Каждая из этих кривых может быть представлена в виде многомерного вектора, в котором каждая точка во времени определяет дополнительное измерение. С использованием такого векторного обозначения прямое расширение простых сравнений максимальных значений является нормой разности векторов экспериментальных данных и данных модели.

Понятие нормы устанавливает определение длины вектора. Расстояние между двумя векторами просто представляет собой длину вектора, полученную в результате вычисления разности двух векторов. Обозначение записано в виде , где - обозначение -мерного вектора (, , ..., , ). Для этого примера сравнение максимальных значений называется равномерной нормой или нормой на основе максимальных абсолютных значений. Чтобы расширить значения равномерной нормы, все данные также могут быть представлены с помощью вектора значений , измеряемого в каждый момент времени. Прогнозы модели на тех же временных точках могут быть представлены в виде вектора . Расстояние между этими двумя векторами является нормой разности векторов, или . Оно может быть легко нормализовано как относительная разность с экспериментальными данными с помощью следующего уравнения:

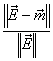. (B.1)

Вектор разностей рассчитывают таким же образом, как в простом примере сравнения максимальных значений двух кривых, принимая разность между экспериментом и моделью в каждый момент времени. Первоначально евклидова норма является наиболее наглядной для вычисления длины

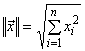. (B.2)

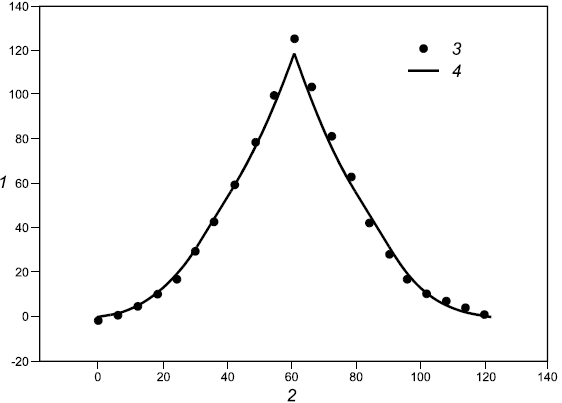
Как сказано далее, другие геометрии также могут быть полезны для сравнения в реальном времени. Например, на рисунке В.1 расстояние между двумя векторами составляет 14,1, а относительная разность равна 0,056. Сравнение максимальных значений этих простых кривых обеспечивает точное измерение общего соответствия, почти идентичного с общим сравнением в уравнении (В.1), поскольку эти две кривые были выбраны с отличием только в максимальных значениях. Для более сложных кривых сравнение максимумов может быть не таким точным. Далее приведен ряд примеров.

Тогда как разность и относительная разность 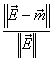обеспечивают измерение расхождения между экспериментальными данными и прогнозами модели, другие расчеты дают полезную информацию об источнике расхождений. При сравнении векторов существуют, как правило, две геометрические компоненты, которые следует учитывать: разность в длине между двумя векторами и (ненулевой) угол между двумя векторами. Скалярное произведение двух векторов является результатом произведения длины двух векторов и косинуса угла между ними:

. (B.3)

или

. (B.4)

Выбор скалярного произведения стандартным произведением точек дает результаты, согласующиеся с типичным евклидово-геометрическим восприятием:

. (B.5)

Для этого уравнения =0,99. Визуально угол между двумя векторами представляет собой измерение точности совпадения форм двух векторов друг с другом. Когда косинус угла достигает единицы, вся форма кривых становится идентичной.

В целом скалярное произведение представляет собой функцию, которая принимает два вектора и возвращает число. Это число может быть вещественным или комплексным; в нашем случае рассмотрены только вещественные скалярные произведения. Следующие аксиомы дают соответствующее определение внутреннего произведения и норму, обеспечивающую необходимые свойства для выполнения векторных вычислений.

Данные аксиомы обеспечивают соответствующие правила для определения скалярного произведения и нормы для других геометрий в дополнение к евклидову пространству. Рассматривают три дополнительных определения геометрии: Хеллингера, секанса и совмещенная от евклидова пространства и секанса. В целях обеспечения совместимости норма может быть определена с точки зрения внутреннего скалярного произведения. Это гарантирует, что в расчетах использованы необходимые соответствующие определения нормы и скалярного произведения. Поскольку угол вектора по отношению к самому себе по определению равен нулю, из уравнения (B.3) следует:

или . (B.6)

Скалярное произведение Хеллингера для функций , при которых 0, определяют на основе первой производной функции:

. (B.7)

Для дискретных векторов оно может быть приближено с первыми разностями, как показано в следующем уравнении:

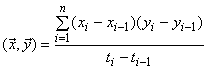. (B.8)

На основе первой производной или касательных кривых скалярное произведение и норма Хеллингера дают чувствительное измерение сравнения формы двух векторов. Вариация скалярного произведения Хеллингера может быть определена на основе секущей, а не касательной, как показано в уравнении

, (B.9)

где определена длина секущей. Ограничение скалярного произведения секущей в виде 0 является интегралом Хеллингера. Для дискретных векторов оно может быть приближено аналогично геометрии Хеллингера:

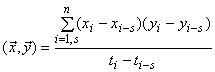. (B.10)

При 1 определение секанса эквивалентно дискретному скалярному произведению Хеллингера. В зависимости от значения или скалярное произведение секанса и норма обеспечивают уровень сглаживания данных и, таким образом, более точно измеряют крупномасштабные различия между векторами. В случае с экспериментальными данными с присущими незначительными помехами или прогнозами модели с численной неустойчивостью, секанс обеспечивает фильтр для сравнения общей функциональной формы кривых без помех. И, наконец, совмещение евклидова скалярного произведения и секанса обеспечивает баланс между упорядочением евклидовой нормы и сравнением функциональной формы с помощью секанса. Согласно приведенным выше аксиомам, сумма двух скалярных произведений также является скалярным произведением. В данном приложении рассмотрена простая взвешенная сумма евклидова скалярного произведения и скалярного произведения секущей

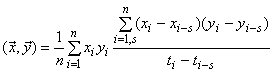. (В.11)

Весовые коэффициенты выравнивают фактор евклидового скалярного произведения и скалярного произведения секущей в сочетании.

На рисунке В.2 приведен простой пример данных, сравниваемых с тремя прогнозами модели. Модель 1 представляет собой простые экспериментальные данные, умноженные на 0,9. Модель 2 имеет такое же максимальное значение, что и модель 1, однако с его сдвигом на минус 25 с. Модель 3 имеет такое же максимальное значение, что модели 1 и модели 2, однако с плато, длящимся 20 с, по центру максимального значения экспериментальных данных. Сравнение только максимальных значений дает возможность продемонстрировать, что все три модели идентичны с относительной разностью 0,1. Очевидно, что данное сравнение не способно отразить различия между тремя моделями. На примере таблицы В.2 показана относительная разница и косинус между векторами экспериментальных данных и прогнозами модели для трех моделей, использующих другие определения для скалярного произведения и нормы.

Все системы метрик характеристик качества выстраивают модели в том же порядке: модель 1 наиболее приближена к экспериментальным данным, за ней следуют модели 2 и 3. Порядок классификации соответствует визуальной интерпретации сравнений. Модель 1, очевидно, является наилучшей, при той же функциональной форме и максимальном значении с правильной привязкой ко времени, однако она немного ниже экспериментальных данных. С другой стороны, модель 2 с настолько смещенным максимальным значением по результатам эксперимента оказывается наихудшей. Несмотря на то что модель 3 не имеет правильного контура максимального значения (удлиненное плато вместо острой вершины), ее форма имеет правильный общий вид, изменяющийся в соответствии с экспериментом.

Относительная разность модели 1 является одинаковой для всех метрик характеристик качества, как и должно быть. По выбору форма вектора модели 1 просто составляет .

Таким образом, относительная разность 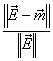независимо от определения нормы, просто составляет 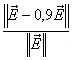или равна 0,1. Аналогично косинус угла между моделью 1 и экспериментом равен 1,0 для всех типов сравнений.

Несмотря на то что евклидова относительная разность и косинус имеют разумные значения для всех моделей, косинус не демонстрирует достаточную дифференциацию между прогнозами модели. Значения Хеллингера и секанса дают большие различия, поскольку они специально сравнивают формы функций экспериментальных данных и данных моделей.

В качестве примера в таблице B.3 приведено сравнение зонной модели CFAST с пятью разными пожарными испытаниями в реальном масштабе с применением данного метода. Они включают следующее:

a) испытание в помещении с одной комнатой и мягкой мебелью в качестве предмета горения было выбрано ввиду его удачных характеристик как реалистичного источника пожара в одном помещении с простой геометрией;

b) огневое испытание в помещении с одной комнатой и мебелью в качестве источника пожара привело к результатам, сходным с результатами первого испытания, с более реалистичным источником пожара;

c) система из трех помещений, для которой приведено среднее значение данных из 11 повторных испытаний с простыми стационарными пожарами с использованием газовой горелки;

d) серия испытаний, проведенных в системе нескольких помещений с более сложными видами пожаров с использованием газовой горелки в отличие от предыдущего набора данных;

e) серия натурных испытаний, проведенных с целью оценить зонные дымозащитные системы, как с обеспечением, так и без обеспечения подпора воздуха на лестничную площадку.

Испытание e) проводилось в восьмиэтажном здании отеля с множеством помещений на каждом этаже и лестничной площадкой, соединяющей все этажи. Выборка данных из этих испытаний использована в настоящем приложении в качестве примеров эквивалентных сравнений, рассчитанных с помощью нормы и скалярного произведения. Подробные данные о геометрии, экспериментальных измерениях и прогнозах модели представлены в [8]. В таблице B.2 приведена норма совмещенной относительной разности для уравнения (B.1) и косинус угла между векторами экспериментальных данных и прогнозами модели для отбора данных из этих пяти испытаний. Для лучшего понимания этих количественных сравнений на рисунке B.3 приведены экспериментальные данные и прогнозы модели для одной из переменных согласно таблице B.2.

На рисунке B.3 продемонстрировано сравнение кривых температур в верхнем слое по результатам испытания в помещении с одной комнатой. В этом испытании доступны два положения для снятия измерений, исходя из экспериментальных данных. Прогнозируемые температуры достаточно схожи с измеренными значениями. Пиковые значения происходят в те же моменты времени с сопоставимыми подъемами и спадами в обеих позициях снятия измерений. В обоих положениях пиковые значения температуры выше, чем в прогнозах модели, при этом одна из позиций несколько выше другой. Как норма относительной разности, так и косинус отражают эти тенденции. Норма относительной разности несколько выше для одного из экспериментальных значений (0,36 против 0,31), что отражает более высокую температуру в данной позиции при снятии измерений. При схожих формах всех кривых косинус дает аналогичные значения для обеих кривых (0,93 и 0,95).

В рассмотренных экспериментах и моделях данные методы обеспечивают возможность количественного сравнения величины и функциональной формы, соответствующей визуальному представлению сравниваемых показателей.

Таблица B.1 - Сравнение "вымышленных" экспериментальных данных с тремя прогнозами модели с использованием различных определений внутреннего скалярного произведения

Таблица B.2 - Сравнение экспериментальных измерений и прогнозов модели для ряда испытаний

1 - измерение; 2 - время; 3 - экспериментальные данные; 4 - прогноз модели

Рисунок B.1 - Простой пример сравнения экспериментальных данных с прогнозом модели

1 - измерение; 2 - время; 3 - данные 6 по отношению к данным 7; 4 - данные 6 по отношению к данным 9; 5 - данные 6 по отношению к данным 11; 6 - данные 6 по отношению к данным 13

Рисунок B.2 - Три возможных прогноза модели для одного примера экспериментальных данных

1 - температура, °С; 2 - время, с; 3 - относительная разность, равная 0,36; косинус, равный 0,95; 4 - относительная разность, равная 0,31; косинус, равный 0,93; 5 - модель; 6 - экспериментальные данные

Рисунок B.3 - Сравнение температур в верхнем слое в испытании с одним помещением

Приложение C
(справочное)

Методы анализа чувствительности

Существует два основных подхода для получения данных чувствительности:

a) локальные методы, которые предоставляют измерения чувствительности для определенного набора входных параметров; при этом необходимо, чтобы измерения повторно проводились для ряда входных параметров с целью получения информации относительно общей производительности модели. Методы конечных разностей могут применять без изменения системы уравнений модели, однако требуется тщательный отбор входных параметров для получения точных оценок. Прямые методы дополняют систему уравнений, решенную посредством модели с использованием уравнений чувствительности. Уравнения чувствительности затем решают совместно с системой уравнений модели для получения значений чувствительности. Необходимо включать прямые методы в структуру пожарной модели, которые редко доступны для уже существующих моделей пожаров;

b) глобальные методы, которые предоставляют измерения чувствительности, усредненные по всему ряду входных параметров. Глобальные методы требуют знания функций плотности вероятностей входных параметров, которые в случае с моделями пожаров, как правило, неизвестны.

Наиболее применимыми являются локальные методы. Глобальные методы используют в тех случаях, когда известна область входных данных, например в расчетах риска при пожарно-техническом анализе.

Даже если чувствительность можно определить и установить различные методы ее расчета, остаются проблемы, связанные с проведением анализа чувствительности. Далее приведен ряд свойств сложных компьютерных моделей, усложняющих анализ чувствительности:

- существует множество входных и выходных переменных;

- в поведении модели могут присутствовать разрывы;

- среди входных переменных могут быть корреляции и связанные с ними безусловные распределения вероятностей, часто отличающиеся от нормальных;

- прогнозы модели представляют собой нелинейные, многомерные, зависящие от времени функции входных переменных;

- относительную важность отдельных входных переменных представляет функция времени.

Кроме того, уравнения чувствительности имеют аналогичные свойства. В выходных и входных данных заданной модели могут быть временные области, в которых выходные данные модели чувствительны к входным данным, а также области, в которых выходные данные модели нечувствительны к одному и тому же параметру.

По меньшей мере два вопроса общего характера могут быть рассмотрены с помощью анализа чувствительности пожарной модели. Первый вопрос - насколько чувствительна модель к тем или иным входным данным? Этот вопрос представляет собой попытку получить общую оценку значимости одних входных данных относительно других входных данных. Для данного вопроса может быть выбрана наиболее широкая область входных данных модели, представляющая собой область применения модели. Последующий анализ выходных данных модели для подобного рода изменений дает представление об относительной значимости этой входной переменной для выбранных выходных данных. Такой анализ дает общую картину поведения модели.

Второй вопрос - насколько точно необходимо задавать конкретные входные данные? Вместо понимания общего поведения модели, это подразумевает под собой попытку получить представление о влиянии неопределенностей в выбранных входных данных на выходные данные модели. Для этого вопроса могут быть изучены небольшие отклонения во входных данных. Если конкретный сценарий представляет интерес, то могут быть изучены отклонения во входных данных для данного сценария.

Средняя относительная разность, таким образом, может быть использована для характеристики чувствительности модели при сравнении отдельных входных и выходных данных.

На рисунке C.1 представлена поверхность отклика для модели пожара, демонстрирующая воздействие изменяющейся мощности тепловыделения и размера вентиляционного отверстия на температуру в верхнем слое. Здесь представлено влияние максимальной мощности тепловыделения и наличие вентиляционного отверстия (в помещении возгорания) на максимальную температуру в верхнем слое. На данном рисунке фактические расчеты модели нормированы по значениям базового сценария, как показано кружками, наложенными на поверхность сетки, сгенерированной сплайновой интерполяцией между точками данных. При взгляде на поверхность сетки становится ясно, что мощность тепловыделения оказывает большее воздействие на максимальную температуру, чем ширина вентиляционного отверстия. Пока горение не ограничивается кислородом, тенденции, видимые на поверхности, соответствуют ожиданиям: температура повышается с ростом мощности тепловыделения и понижается с увеличением ширины вентиляционного отверстия. Влияние как мощности тепловыделения, так и вентиляционного отверстия, безусловно, не является линейным.

- нормированная пиковая температура; - нормированная ширина вентиляционного отверстия; - нормированная скорость тепловыделения

Рисунок C.1 - Поверхность отклика пожарной модели для характеристики чувствительности модели при сравнении отдельных входных и выходных данных

Воздействие изменения скорости выделения тепла и размера вентиляционного отверстия на температуру верхнего слоя.

Численные методы были разработаны для определения чувствительности сложных моделей при необходимости оптимизировать выборку, т.е. в тех условиях, когда расчетное время имеет решающее значение, и масштабные вычисления, таким образом, становятся чрезмерно дорогими. Многие важные применения в пожарно-техническом анализе представлены дорогими в вычислительном отношении модельными уравнениями, например уравнениями Навье-Стокса для потоков жидкости и других уравнений переноса. Большинство из этих дорогих систем расчета в значительной степени нелинейны. Допустимо применение линейных приближений (см. [5]), однако результаты могут быть ненадежными, и, следовательно, рекомендуется использовать моделирование методом Монте-Карло, например предложенное в дополнении 1 (см. [6]). Такие модели успешно применялись к моделям пожара для анализа чувствительности, особенно к зонным моделям. Однако методы Монте-Карло основаны на большом количестве оценок модели и тем самым не имеют практического применения. В результате сообщения о неопределенности в измерениях посредством дорогих в вычислительном отношении моделях, как правило, либо отсутствуют, либо основаны на грубых приближениях. Были приняты альтернативные методы по снижению количества вычислений (методы выборки).

В целях локальной оценки для многих методов выборки установлены специальные требования, ограничения или допущения (входные данные должны быть независимыми, выходная величина может иметь локальное приближение как полиномиальная функция входных величин), которые могут ограничивать их применение. Для того чтобы справиться с трудностями в оценке чувствительности с участием нелинейных дорогих в вычислительном отношении моделей, в настоящее время используют два основных подхода: методы разумной выборки и моделирование замещением.

Методы разумной выборки, такие как полиномиальный хаос (расширение хаоса Винера) и выборка латинского гиперкуба, значительно сокращают число оценок функций и, как следствие, вычислительные затраты, необходимые для оценки неопределенности по сравнению со случайной выборкой.

В моделировании замещением дешевые в вычислительном отношении модели заменяют дорогие модели; затем используют статистическое моделирование для учета неизбежных погрешностей, вносимых замещающими моделями, методами разумной выборки и моделированием замещением. В качестве примера можно соотнести модель вычислительной гидродинамики с зонной моделью, далее исследовать чувствительность зонной модели. В этом случае чувствительность входных данных, которые похожи в обеих моделях, должна быть согласована.

В программе по оценке ранее было указано, что чувствительность также играет важную роль. Могут использовать различные программы по оценке чувствительности моделей с использованием метода Монте-Карло и усеченные методы выборки. Методы, применяемые для проведения анализа чувствительности, не эквивалентны в отношении оценки и расчета расходов. Все они различаются с точки зрения возможностей, ограничений и расчета затрат.

Основными используемыми методами являются следующие:

- нормализованный коэффициент регрессии ряда SRRC, вариант программы оценки дисперсии линейного нормализованного коэффициента регрессии SRC, адаптированный для решения нелинейных задач;

- индексы Соболя для оценки показателей чувствительности первого порядка по количеству;

- анализ чувствительности амплитуды Фурье FAST, в котором многомерный анализ сведен к одномерной задаче в пространстве Фурье;

- местные полиномиальные сглаживатели, в которых аппроксимация модели осуществлена путем полиномиального приближения к точке анализа.

Приложение D
(справочное)

Методика обеспечения контроля качества

D.1 Общие положения

В настоящем приложении рассмотрена методология обеспечения качества в общем контексте разработки программного обеспечения.

Процесс оценки представлен на рисунке D.1 (см. также 5.6) и в D.2-D.6.

Рисунок D.1 - Диаграмма согласно ГОСТ Р ИСО/МЭК 25040 [8]

D.2 Определение требований оценки

D.2.1 Определение цели оценки

Цель оценки программного продукта заключается в сравнении качества программного продукта с требованиями к качеству, которые отражают потребности пользователя, или даже в выборе программного продукта путем сравнения различных программных продуктов, или в классификации продукта в соответствии с его конкурентами. Эта общая цель может быть более точно изложена при рассмотрении вопроса с точки зрения оценки программного продукта, например приобретения, в процессе разработки или в условиях эксплуатации.

D.2.2 Идентификация типа программной продукции, подлежащей оценке

Тип программного продукта оценивают в зависимости от задачи оценки. В первую очередь производящий оценку должен классифицировать программные продукты, подвергаемые оценке, как промежуточные (в процессе жизненного цикла разработки) или конечные. Оцениваемые программные продукты могут быть измерены с помощью:

- внешних метрик характеристик качества, когда программный продукт является частью целой системы аппаратного/программного обеспечения, находящейся в условиях эксплуатации;

- внутренних метрик характеристик качества, которые могут применять для измерения внутренних свойств программного обеспечения (например, спецификации или исходного кода);

- метрик характеристик качества при применении, которые измеряют эффективность использования программного обеспечения в заданной среде.

D.2.3 Спецификация качественной модели

Качественная модель, выбранная для оценки, представляет собой образец для определения требований к программному обеспечению. На данном этапе оценки указаны требования к соответствующим качественным характеристикам, приведенные по порядку в соответствии с потребностями пользователя.

D.3 Спецификация оценки

D.3.1 Выбор метрик характеристик качества

Количественная спецификация и измерение требований к качеству программного продукта могут быть проведены только с помощью метрик характеристик качества, которые связаны с ожидаемыми качественными характеристиками.

Метрики характеристик качества могут быть следующих типов:

a) внутренние, например связанные с архитектурой программного продукта и позволяющие прогнозировать качество конечного продукта;

b) внешние, например, поддающиеся измерению, когда программный продукт находится в эксплуатации;

c) метрики качества при применении, для оценки результатов использования программного продукта.

Выбор используемых показателей во время оценки программного продукта зависит от цели оценки, выбранных качественных характеристик и от того, насколько просто и экономично применение измерений. Метрики, используемые для сравнения, также должны быть значимыми и достаточно точными, чтобы обеспечить достоверные сравнения. Это означает, что измерения должны быть объективными, основанными на опыте, проведенными с использованием действительной шкалы и воспроизводимыми.

D.3.2 Определение уровней градации для метрик характеристик качества

Для каждой выбранной метрики характеристик качества должны быть определены рейтинговые значения по соответствующей шкале, на которой указан требуемый уровень измеряемого параметра. На принятой шкале могут быть указаны пределы для каждого параметра, определяющие степень соответствия, например недопустимый, минимально допустимый, приемлемый для целевой области значений или превышающий требования.

D.3.3 Определение критериев оценки

Критерии оценки не требуют в обязательном порядке суммирования значений измерений, чтобы получить уникальный показатель, представляющий качество программного продукта, поскольку качество характеризуется соблюдением установленных требований. Таким образом, стоимость и режим работы могут быть подобраны к каждому установленному требованию и его измеренному значению. Когда процесс оценки используют для выбора определенного программного продукта, может потребоваться создание модели, представляющей воспринимаемую коммерческую ценность каждого программного продукта по измеренным значениям, с целью обеспечения более объективного сравнения.

D.4 Расчет оценки

Документирование методов оценки и создание проекта плана требуют решения задач, таких как:

- технические ограничения, связанные с измерениями или верификацией;

- методы оценки для каждого измерения или верификации, которые подлежат документированию;

- идентификация программных средств, используемых для измерений;

- идентификация компонентов программных продуктов, на которых должен быть применен данный метод;

- спецификация интерпретации результатов, при необходимости;

- описание окружающей среды.

Оптимизация плана оценки, решающего такие вопросы, как проверка проекта плана оценки с целью избежать дублирования действий лица, проводящего оценку.

Планирование действий по оценке с учетом имеющихся ресурсов для решения вопросов, таких как:

- измерение и распределение порядка запланированных действий, а также их учет;

- график доставки программного продукта и его компонентов;

- взаимодействие между лицом, проводящим оценку, и разработчиком;

- обеспечение доступа к местам разработки и эксплуатации.

Примечание - При подготовке плана оценки рекомендуется воспользоваться ГОСТ Р ИСО/МЭК 25040, для того чтобы получить более широкое представление о данном вопросе.

D.5 Выполнение оценки

D.5.1 Измерение

Выбранные метрики следует применять к программному продукту, что в результате позволит получить значения на шкале метрик.

D.5.2 Сравнение с критериями

Измеренные значения сравнивают с критериями, установленными в спецификации. Для измерений конечного продукта значения сравнивают с целевыми значениями.

Измеренные значения должны использовать, чтобы определить:

- каждый недостаток программного продукта и способ его устранения;

- любые дополнительные оценки, необходимые для устранения любых выявленных недостатков; дополнительная оценка может, например, подтвердить отсутствие недостатков, или использоваться для верификации правильной и приемлемой производительности системы программного обеспечения сразу после того, как в нее были внесены изменения для исправления недостатков;

- стоит ли ограничивать или контролировать использование программного продукта и, в данном случае, воздействует ли ограничение, например, на обязательные требования, требует ли оно дополнительной работы по оценке или воздействует на характер применения, бюджет или режим работы;

- любые исключения из области применения оценки и/или ограничения по результатам для каждой оценки, такие как: "В данную оценку не входит подробный обзор функциональных возможностей программного продукта";

- объединенные результаты всех мероприятий по оценке, чтобы предоставить общий вывод по оценке программного продукта.

D.5.3 Оценка результатов

При осуществлении деятельности по оценке суммируют набор расчетных значений и формируют положение о степени, в которой программный продукт отвечает требованиям качества. Данную итоговую оценку затем сравнивают с другими аспектами, такими как время и стоимость. Наконец, на основе управленческих критериев принимают положительное или отрицательное решение относительно применения программного продукта либо о его выпуске или отказе от выпуска. Результаты оценки влияют на определенные шаги жизненного цикла разработки программного обеспечения: например, "должны ли требования быть изменены или необходимы ли дополнительные ресурсы для процесса разработки?"

Сделанные выводы объясняются двумя взаимодополняющими подходами:

a) путем формализации выводов, используя "положение о соответствии требованиям", которое разъясняет, каким образом выполнено каждое требование;

b) принятия окончательного решения относительно использования программного продукта и рассмотрения возможных альтернатив: например, если программный продукт не отвечает требованиям заказчика, рассматривается вопрос об изменении продукта или изменении требований.

D.5.4 Другие аспекты

Лицо, проводящее оценку, несет ответственность за выводы по оценке, однако оно вправе производить окончательную оценку, только если это указано в спецификации оценки. Оценщик, как правило, предоставляет заказчику отчет по оценке, который может содержать определенные заключения, после чего заказчик завершает оценку на основе данного отчета. Это обусловлено тем, что окончательная оценка может учитывать стратегические решения организации, такие как стоимость, изменения, необходимые для реализации, и время поставки.

D.6 Пример руководства (согласно ГОСТ Р ИСО/МЭК 25040)

D.6.1 Выбор метрик характеристик качества и критериев измерения

Основные критерии, по которым делают выбор метрик характеристик качества, зависят от коммерческих целей программного продукта и потребностей оценщика. Потребности обозначены критериями измерений. Модель, приведенная в ГОСТ Р ИСО/МЭК 25040, поддерживает различные виды оценочных требований, например:

- пользователь или его организация могут оценивать пригодность программного продукта с точки зрения метрик характеристик качества при применении;

- покупатель может оценивать программный продукт по нормативным значениям внешних измерений функциональности, надежности, пригодности и эффективности или качества при применении;

- лицо, осуществляющее техническую поддержку, может оценивать программный продукт с помощью метрик характеристик качества для эксплуатационной надежности;

- лицо, ответственное за внедрение программного обеспечения в различной среде, может оценивать программный продукт с помощью метрик характеристик качества портативности;

- разработчик может оценивать программный продукт по нормативным значениям с помощью внутренних измерений любой из качественных характеристик.

Примечание - Требования и руководство по выбору метрик характеристик качества и критериев измерения для оценки программного продукта приведены в ГОСТ Р ИСО/МЭК 25040.

D.6.2 Уровни ранжирования для метрик характеристик качества

Измеримые характеристики могут быть количественно определены с использованием метрик характеристик качества. Результат, т.е. измеренное значение, отображен на шкале. Данное значение само по себе не показывает уровень соответствия требованиям. Для этой цели необходимо разделить шкалу на области, соответствующие различным степеням удовлетворения требований, например:

- деление шкалы на две категории - неудовлетворительно и удовлетворительно;

- деление шкалы на четыре категории, ограниченные текущим уровнем существующего или альтернативного продукта, наихудшим случаем и запланированным уровнем. Текущий уровень указывают с целью контроля того, что новая система не уступает существующей системе. Запланированный уровень представляет собой значение, которое считается достижимым с учетом имеющихся ресурсов. Уровень наихудшего случая определяет границу приемлемости продукта для пользователя в том случае, если продукт не выполняет требований запланированного уровня (см. рисунок D.2).

Рисунок D.2 - Уровни ранжирования метрик характеристик качества

D.6.3 Метрики характеристик качества для оценки: установка критериев оценки

Спецификации требований к качеству программного обеспечения должны быть определены с помощью соответствующей, четко определенной модели качества. Для этой цели следует использовать модель качества и определения, приведенную в ГОСТ Р ИСО/МЭК 25040, если нет необходимости использовать другую модель.

Для оценки качества продукта необходимо суммировать результаты оценки различных характеристик. Для этой цели лицо, проводящее оценку, должно подготовить процедуру с отдельными критериями для различных характеристик качества, каждый из которых может быть установлен в соответствии с отдельными подхарактеристиками, или взвешенной комбинацией подхарактеристик. Данная процедура, как правило, включает в себя и другие аспекты, такие как время и стоимость, которые вносят свой вклад в оценку качества программного продукта в конкретной среде.

Приложение ДА
(справочное)

Сведения о соответствии ссылочных национальных стандартов международным стандартам, использованным в качестве ссылочных в примененном международном стандарте

Таблица ДА.1

Библиография

Электронный текст документа

и сверен по:

, 2019