ГОСТ Р 34.10-2012
Группа П85
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Информационная технология
КРИПТОГРАФИЧЕСКАЯ ЗАЩИТА ИНФОРМАЦИИ
Процессы формирования и проверки электронной цифровой подписи
Information technology. Cryptographic data security. Generation and verification processes of electronic digital signature
ОКС 35.040
ОКСТУ 5001
Дата введения 2013-01-01
Предисловие
1 РАЗРАБОТАН Центром защиты информации и специальной связи ФСБ России с участием Открытого акционерного общества "Информационные технологии и коммуникационные системы" (ОАО "ИнфоТеКС")
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 26 "Криптографическая защита информации"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 7 августа 2012 г. N 215-ст
4 ВЗАМЕН ГОСТ Р 34.10-2001
5 ПЕРЕИЗДАНИЕ. Сентябрь 2018 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Настоящий стандарт содержит описание процессов формирования и проверки электронной цифровой подписи (ЭЦП), реализуемой с использованием операций в группе точек эллиптической кривой, определенной над конечным простым полем.
Необходимость разработки настоящего стандарта вызвана потребностью в реализации электронной цифровой подписи разной степени стойкости в связи с повышением уровня развития вычислительной техники. Стойкость электронной цифровой подписи основывается на сложности вычисления дискретного логарифма в группе точек эллиптической кривой, а также на стойкости используемой хэш-функции по ГОСТ Р 34.11-2012.
Настоящий стандарт разработан с учетом терминологии и концепций международных стандартов ИСО 2382-2* [1], ИСО/МЭК 9796* [2]-[3], ИСО/МЭК 14888* [4]-[7] и ИСО/МЭК 10118* [8]-[11].
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
1 Область применения
Настоящий стандарт определяет схему электронной цифровой подписи (ЭЦП) (далее - цифровая подпись), процессы формирования и проверки цифровой подписи под заданным сообщением (документом), передаваемым по незащищенным телекоммуникационным каналам общего пользования в системах обработки информации различного назначения.
Внедрение цифровой подписи на основе настоящего стандарта повышает по сравнению с ранее действовавшей схемой цифровой подписи уровень защищенности передаваемых сообщений от подделок и искажений.
Настоящий стандарт рекомендуется применять при создании, эксплуатации и модернизации систем обработки информации различного назначения.
2 Нормативные ссылки
В настоящем стандарте использована ссылка на следующий стандарт:
ГОСТ Р 34.11-2012 Информационная технология. Криптографическая защита информации. Функция хэширования
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
3 Термины, определения и обозначения
3.1 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
3.1.1
дополнение (appendix): Строка бит, формируемая из цифровой подписи и произвольного текстового поля. [ИСО/МЭК 14888-1:2008 [4]] |
3.1.2
ключ подписи (signature key): Элемент секретных данных, специфичный для субъекта и используемый только данным субъектом в процессе формирования цифровой подписи. [ИСО/МЭК 14888-1:2008 [4]] |
3.1.3
ключ проверки подписи (verification key): Элемент данных, математически связанный с ключом подписи и используемый проверяющей стороной в процессе проверки цифровой подписи. [ИСО/МЭК 14888-1:2008 [4]] |
3.1.4
параметр схемы ЭЦП (domain parameter): Элемент данных, общий для всех субъектов схемы цифровой подписи, известный или доступный всем этим субъектам. [ИСО/МЭК 14888-1:2008 [4]] |
3.1.5
подписанное сообщение (signed message): Набор элементов данных, состоящий из сообщения и дополнения, являющегося частью сообщения. [ИСО/МЭК 14888-1:2008 [4]] |
3.1.6
последовательность псевдослучайных чисел (pseudo-random number sequence): Последовательность чисел, полученная в результате выполнения некоторого арифметического (вычислительного) процесса, используемая в конкретном случае вместо последовательности случайных чисел. [ИСО 2382-2:1976 [1]] |
3.1.7
последовательность случайных чисел (random number sequence): Последовательность чисел, каждое из которых не может быть предсказано (вычислено) только на основе знания предшествующих ему чисел данной последовательности. [ИСО 2382-2:1976 [1]] |
3.1.8
процесс проверки подписи (verification process): Процесс, в качестве исходных данных которого используются подписанное сообщение, ключ проверки подписи и параметры схемы ЭЦП, результатом которого является заключение о правильности или ошибочности цифровой подписи. [ИСО/МЭК 14888-1:2008 [4]] |
3.1.9
процесс формирования подписи (signature process): Процесс, в качестве исходных данных которого используются сообщение, ключ подписи и параметры схемы ЭЦП, а в результате формируется цифровая подпись. [ИСО/МЭК 14888-1:2008, [4]] |
3.1.10 свидетельство (witness): Элемент данных, представляющий соответствующее доказательство достоверности (недостоверности) подписи проверяющей стороне.
3.1.11
случайное число (random number): Число, выбранное из определенного набора чисел таким образом, что каждое число из данного набора может быть выбрано с одинаковой вероятностью. [ИСО 2382-2:1976 [1]] |
3.1.12
сообщение (message): Строка бит произвольной конечной длины. [ИСО/МЭК 14888-1:2008 [4]] |
3.1.13
хэш-код (hash-code): Строка бит, являющаяся выходным результатом хэш-функции. [ИСО/МЭК 14888-1:2008 [4]] |
3.1.14
хэш-функция (collision-resistant hash-function): Функция, отображающая строки бит в строки бит фиксированной длины и удовлетворяющая следующим свойствам: 1) по данному значению функции сложно вычислить исходные данные, отображаемые в это значение; 2) для заданных исходных данных сложно вычислить другие исходные данные, отображаемые в то же значение функции; 3) сложно вычислить какую-либо пару исходных данных, отображаемых в одно и то же значение. [ИСО/МЭК 14888-1:2008 [4]] |
Примечания
1 Применительно к области электронной цифровой подписи свойство по перечислению 1) подразумевает, что по известной электронной цифровой подписи невозможно восстановить исходное сообщение; свойство по перечислению 2) подразумевает, что для заданного подписанного сообщения трудно подобрать другое (фальсифицированное) сообщение, имеющее ту же электронную цифровую подпись; свойство по перечислению 3) подразумевает, что трудно подобрать какую-либо пару сообщений, имеющих одну и ту же подпись.
2 В настоящем стандарте в целях сохранения терминологической преемственности с действующими отечественными нормативными документами и опубликованными научно-техническими изданиями установлено, что термины "хэш-функция", "криптографическая хэш-функция", "функция хэширования" и "криптографическая функция хэширования" являются синонимами.
3.1.15
[электронная цифровая] подпись (signature); ЭЦП: Строка бит, полученная в результате процесса формирования подписи. [ИСО/МЭК 14888-1:2008 [4]] |
Примечания
1 Строка бит, являющаяся подписью, может иметь внутреннюю структуру, зависящую от конкретного механизма формирования подписи.
2 В настоящем стандарте в целях сохранения терминологической преемственности с действующими отечественными нормативными документами и опубликованными научно-техническими изданиями установлено, что термины "электронная подпись", "цифровая подпись" и "электронная цифровая подпись" являются синонимами.
3.2 Обозначения
В настоящем стандарте применены следующие обозначения:
- множество всех двоичных векторов длиной | |
- множество всех двоичных векторов произвольной конечной длины; | |
- множество всех целых чисел; | |
- простое число, | |
- конечное простое поле, представляемое как множество из | |
| - минимальное неотрицательное число, сравнимое с |
- сообщение пользователя, | |
| - конкатенация (объединение) двух двоичных векторов; |
| - коэффициенты эллиптической кривой; |
- порядок группы точек эллиптической кривой; | |
- порядок подгруппы группы точек эллиптической кривой; | |
- нулевая точка эллиптической кривой; | |
- точка эллиптической кривой порядка | |
- целое число - ключ подписи; | |
- точка эллиптической кривой - ключ проверки подписи; | |
- цифровая подпись под сообщением |
;
4 Общие положения
Общепризнанная схема (модель) цифровой подписи (см. ИСО/МЭК 14888-1 [4]) охватывает следующие процессы:
- генерация ключей (подписи и проверки подписи);
- формирование подписи;
- проверка подписи.
В настоящем стандарте процесс генерации ключей (подписи и проверки подписи) не рассмотрен. Характеристики и способы реализации данного процесса определяются вовлеченными в него субъектами, которые устанавливают соответствующие параметры по взаимному согласованию.
Механизм цифровой подписи определяется посредством реализации двух основных процессов (см. раздел 6):
- формирование подписи (см. 6.1);
- проверка подписи (см. 6.2).
Цифровая подпись предназначена для аутентификации лица, подписавшего электронное сообщение. Кроме того, использование ЭЦП предоставляет возможность обеспечить следующие свойства при передаче в системе подписанного сообщения:
- осуществление контроля целостности передаваемого подписанного сообщения;
- доказательное подтверждение авторства лица, подписавшего сообщение;
- защита сообщения от возможной подделки.
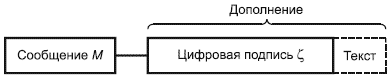
Схематическое представление подписанного сообщения показано на рисунке 1.
|
Рисунок 1 - Схема подписанного сообщения
Поле "Текст", показанное на данном рисунке и дополняющее поле "Цифровая подпись", может, например, содержать идентификаторы субъекта, подписавшего сообщение, и/или метку времени.
Установленная в настоящем стандарте схема цифровой подписи должна быть реализована с использованием операций группы точек эллиптической кривой, определенной над конечным простым полем, а также хэш-функции.
Криптографическая стойкость данной схемы цифровой подписи основывается на сложности решения задачи дискретного логарифмирования в группе точек эллиптической кривой, а также на стойкости используемой хэш-функции. Алгоритмы вычисления хэш-функции установлены в ГОСТ Р 34.11-2012.
Параметры схемы цифровой подписи, необходимые для ее формирования и проверки, определены в 5.2. В настоящем стандарте предусмотрена возможность выбора одного из двух вариантов требований к параметрам.
Настоящий стандарт не определяет процесс генерации параметров схемы цифровой подписи. Конкретный алгоритм (способ) реализации данного процесса определяется субъектами схемы цифровой подписи исходя из требований к аппаратно-программным средствам, реализующим электронный документооборот.
Цифровая подпись, представленная в виде двоичного вектора длиной 512 или 1024 бита, должна вычисляться с помощью определенного набора правил, изложенных в 6.1.
Набор правил, позволяющих принять либо отвергнуть цифровую подпись под полученным сообщением, установлен в 6.2.
5 Математические объекты
Для определения схемы цифровой подписи необходимо описать базовые математические объекты, используемые в процессах ее формирования и проверки. В данном разделе установлены основные математические определения и требования, предъявляемые к параметрам схемы цифровой подписи.
5.1 Математические определения
Эллиптической кривой , определенной над конечным простым полем
(где
3 - простое число), называется множество пар чисел (
,
),
,
, удовлетворяющих уравнению
, (1)
где ,
и 
не сравнимо с нулем по модулю .
Инвариантом эллиптической кривой называется величина , удовлетворяющая уравнению
. (2)
Пары , где
,
- элементы поля
, удовлетворяющие уравнению (1), называются "точками эллиптической кривой
";
и
- соответственно
- и
- координатами точки.
Точка эллиптической кривой обозначается 
или просто . Две точки эллиптической кривой равны, если равны их соответствующие
- и
-координаты.
На множестве точек эллиптической кривой операцию сложения обозначают знаком "+". Для двух произвольных точек
и 
эллиптической кривой рассматривают несколько случаев.
Для точек и
, координаты которых удовлетворяют условию
, их суммой называется точка 
, координаты которой определяются сравнениями
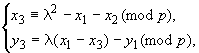(3)
где 
.
Если выполнены равенства 
и 
, то координаты точки определяются следующим образом:
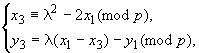(4)
где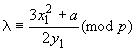 
.
Если выполнены условия 
и 
, то сумма точек и
называется нулевой точкой
без определения ее
- и
-координат. В этом случае точка
называется отрицанием точки
. Для нулевой точки
выполнены равенства
, (5)
где - произвольная точка эллиптической кривой
.
Относительно введенной операции сложения множество точек эллиптической кривой вместе с нулевой точкой образуют конечную абелеву (коммутативную) группу порядка
, для которого выполнено неравенство
. (6)
Точка называется "точкой кратности
" или просто "кратной точкой эллиптической кривой
", если для некоторой точки
выполнено равенство
. (7)
5.2 Параметры цифровой подписи
Параметрами схемы цифровой подписи являются:
- простое число - модуль эллиптической кривой;
- эллиптическая кривая , задаваемая коэффициентами
,
;
- целое число - порядок группы точек эллиптической кривой
;
- простое число - порядок циклической подгруппы группы точек эллиптической кривой
, для которого выполнены следующие условия:
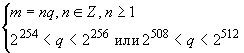; (8)
- точка 
эллиптической кривой , с координатами (
,
), удовлетворяющая равенству
;
- хэш-функция 
, отображающая сообщения, представленные в виде двоичных векторов произвольной конечной длины, в двоичные векторы длины бит. Хэш-функция определена в ГОСТ Р 34.11-2012. Если
, то 256. Если
, то 512.
Каждый пользователь схемы цифровой подписи должен обладать личными ключами:
- ключом подписи - целым числом , удовлетворяющим неравенству
;
- ключом проверки подписи - точкой эллиптической кривой с координатами (
,
), удовлетворяющей равенству
.
К приведенным выше параметрам схемы цифровой подписи предъявляют следующие требования:
- должно быть выполнено условие 
для всех целых 1, 2, ...
, где
31, если
и 131, если
;
- должно быть выполнено неравенство 
;
- инвариант кривой должен удовлетворять условию: 
0 и 
1728.
5.3 Двоичные векторы
Для определения процессов формирования и проверки цифровой подписи необходимо установить соответствие между целыми числами и двоичными векторами длины бит.
Рассмотрим следующий двоичный вектор длиной бит, в котором младшие биты расположены справа, а старшие - слева:
, (9)
где ,
0, ...,
равно либо 1, либо 0.
Число 
соответствует двоичному вектору , если выполнено равенство
. (10)
Для двух двоичных векторов
,
(11)
,
соответствующих целым числам и
, операция конкатенации (объединения) определяется следующим образом:
. (12)
Объединение представляет собой двоичный вектор длиной бит, составленный из компонент векторов
и
.
Формулы (11) и (12) определяют способ разбиения двоичного вектора 
длиной бит на два двоичных вектора длиной
бит, конкатенацией которых он является.
6 Основные процессы
В данном разделе определены процессы формирования и проверки цифровой подписи под сообщением пользователя.
Для реализации данных процессов необходимо, чтобы всем пользователям были известны параметры схемы цифровой подписи, соответствующие требованиям 5.2.
Кроме того, каждый пользователь должен иметь ключ подписи и ключ проверки подписи
, которые также должны соответствовать требованиям 5.2.
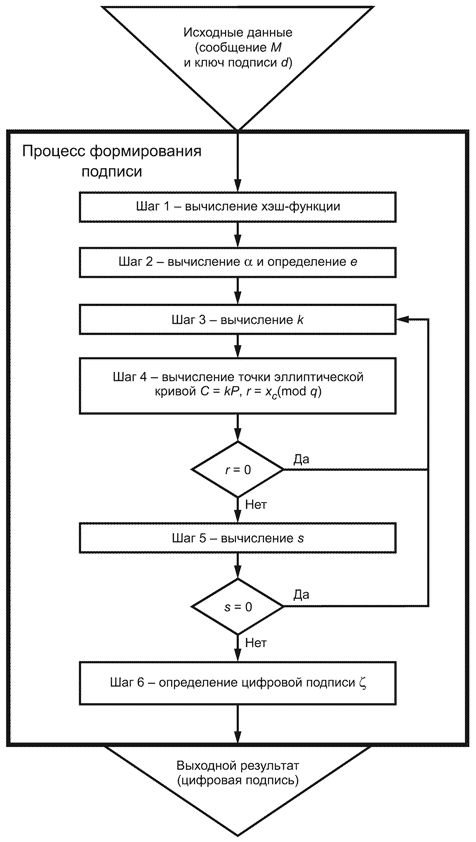
6.1 Формирование цифровой подписи
Для получения цифровой подписи под сообщением 
необходимо выполнить следующие действия (шаги) по алгоритму I:
Шаг 1 - вычислить хэш-код сообщения
. (13)
Шаг 2 - вычислить целое число , двоичным представлением которого является вектор
, и определить
. (14)
Если 0, то определить
1.
Шаг 3 - сгенерировать случайное (псевдослучайное) целое число , удовлетворяющее неравенству
. (15)
Шаг 4 - вычислить точку эллиптической кривой 
и определить
, (16)
где -
-координата точки
.
Если 0, то вернуться к шагу 3.
Шаг 5 - вычислить значение
. (17)
Если 0, то вернуться к шагу 3.
Шаг 6 - вычислить двоичные векторы и
, соответствующие
и
, и определить цифровую подпись
как конкатенацию двух двоичных векторов.
Исходными данными этого процесса являются ключ подписи и подписываемое сообщение
, а выходным результатом - цифровая подпись
.
Схема процесса формирования цифровой подписи приведена на рисунке 2.
|
Рисунок 2 - Схема процесса формирования цифровой подписи
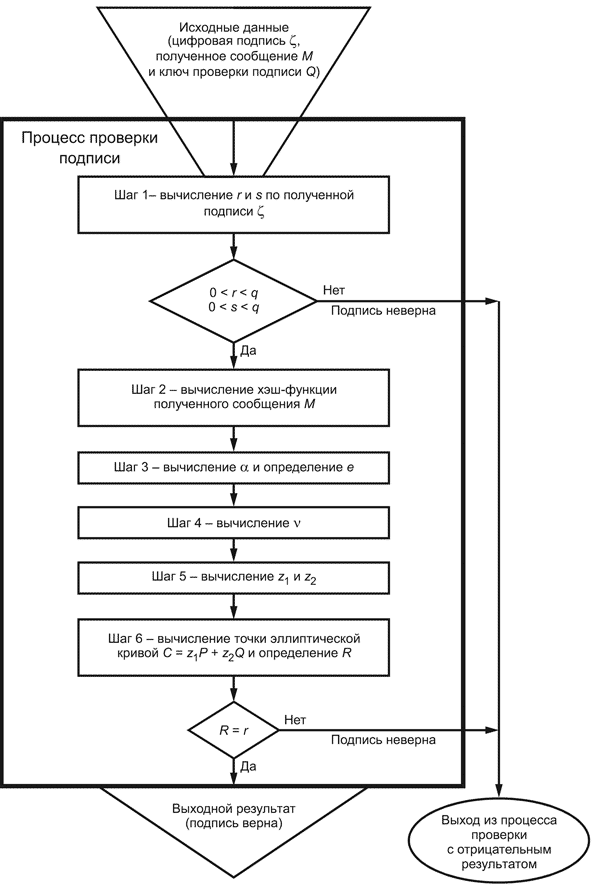
6.2 Проверка цифровой подписи
Для проверки цифровой подписи под полученным сообщением
необходимо выполнить следующие действия (шаги) по алгоритму II:
Шаг 1 - по полученной подписи вычислить целые числа
и
. Если выполнены неравенства
, 
, то перейти к следующему шагу. В противном случае подпись неверна.
Шаг 2 - вычислить хэш-код полученного сообщения :
. (18)
Шаг 3 - вычислить целое число , двоичным представлением которого является вектор
, и определить
. (19)
Если 0, то определить
1.
Шаг 4 - вычислить значение
. (20)
Шаг 5 - вычислить значения
, 
. (21)
Шаг 6 - вычислить точку эллиптической кривой 
и определить
, (22)
где -
-координата точки
.
Шаг 7 - если выполнено равенство , то подпись принимается, в противном случае - подпись неверна.
Исходными данными этого процесса являются подписанное сообщение , цифровая подпись
и ключ проверки подписи
, а выходным результатом - свидетельство о достоверности или ошибочности данной подписи.
Схема процесса проверки цифровой подписи приведена на рисунке 3.
|
Рисунок 3 - Схема процесса проверки цифровой подписи
Приложение А
(справочное)
Контрольные примеры
Приводимые ниже значения параметров , a, b,
,
,
, а также значения ключей подписи и проверки подписи
и
рекомендуется использовать только для проверки корректной работы конкретной реализации алгоритмов, описанных в настоящем стандарте.
Все числовые значения приведены в десятичной и шестнадцатеричной записи. Нижний индекс в записи числа обозначает основание системы счисления. Символ "\\" обозначает перенос числа на новую строку. Например, запись
12345\\
67890
499602D2
представляет целое число 1234567890 в десятичной и шестнадцатеричной системах счисления соответственно.
А.1 Пример 1
А.1.1 Параметры схемы цифровой подписи
Для формирования и проверки цифровой подписи должны быть использованы следующие параметры (см. 5.2).
А.1.1.1 Модуль эллиптической кривой
В данном примере параметру присвоено следующее значение:
57896044618658097711785492504343953926\\
634992332820282019728792003956564821041,
8000000000000000000000000000000000000000000000000000000000000431
А.1.1.2 Коэффициенты эллиптической кривой
В данном примере параметры a и b принимают следующие значения:
a=7,
a=7,
b=43308876546767276905765904595650931995\\
9421117944510395832529688420338495804145FBFF498AA938CE739B8E022FBAFEF40563F6E6A3472FC2A514C0CE9DAE23B7E
А.1.1.3 Порядок группы точек эллиптической кривой
В данном примере параметр принимает следующее значение:
5789604461865809771178549250434395392\\
70829345837254506223809735921376310696198000000000000000000000000000000150FE8A1892976154C59CFC193ACCF5B3
А.1.1.4 Порядок циклической подгруппы группы точек эллиптической кривой
В данном примере параметр принимает следующее значение:
5789604461865809771178549250434395392\\
70829345837254506223809735921376310696198000000000000000000000000000000150FE8A1892976154C59CFC193ACCF5B3
А.1.1.5 Коэффициенты точки эллиптической кривой
В данном примере координаты точки принимают следующие значения:
2
2
40189740565390375033354494229370597\\
756357393899055450806909793652134315662808E2A8A0E65147D4BD6316030E16D19\\
C85C97F0A9CA267122B96ABBCEA7E8FC8
А.1.1.6 Ключ подписи
В данном примере считается, что пользователь обладает следующим ключом подписи :
554411960653632461263556241303241831\\
965767092223400165721080977500060975255447A929ADE789BB9BE10ED359DD39A72C\\
11В60961F49397EEE1D19СЕ9891ЕС3В28
А.1.1.7 Ключ проверки подписи
В данном примере считается, что пользователь обладает ключом проверки подписи , координаты которого имеют следующие значения:
57520216126176808443631405023338071\\
1766301049063136321828967413422066048594037F2B49E270DB6D90D8595BEC458B5\\
0C58585BA1D4E9B788F6689DBD8E56FD80B17614944419213781543809391949654080\\
03194266204536363926070984785943828676399426F1B489D6701DD185С8413A977B3\\
CBBAF64D1C593D26627DFFB101A87FF77DA
А.1.2 Процесс формирования цифровой подписи (алгоритм I)
Пусть после выполнения шагов 1-3 по алгоритму I (см. 6.1) были получены следующие числовые значения:
2079889367447645201713406156150827013\\
06371425153796532899526172526614688724212DFBC1B372D89A1188C09C52E0EE\\
C61FCE52032AB1022E8E67ECE6672B043EE5538541376773484637314038411479966192\\
4150400343430202071296083852889319623339577105C9B20BCD3122823C8CF6FCC\\
7B956DE33814E95B7FE64FED924594DCEAB3
При этом кратная точка 
имеет координаты:
297009809158179528743712049839382569\\
9042275210799431965163268798205921093339541AA28D2F1AB148280CD9ED56FED\\
A41974053554A42767B83AD043FD39DC0493328425352786846634770946653225170845\\
06804721032454543268132854556539274060910489С375А9941А3049Е33В34361DD\\
204172AD98C3E5916DE27695D22A61FAE46E
Параметр 
принимает значение:
297009809158179528743712049839382569\\
9042275210799431965163268798205921093339541AA28D2F1AB148280CD9ED56FED\\
A41974053554A42767B83AD043FD39DC0493
Параметр 
принимает значение:
57497340027008465417892531001914703\\
84552270426490985639337189991755158395521456C64BA4642A1653C235A98A60249BCD6D3F746B631DF928014F6C5BF9C40
А.1.3 Процесс проверки цифровой подписи (алгоритм II)
Пусть после выполнения шагов 1-3 по алгоритму II (см. 6.2) были получены следующие числовые значения:
2079889367447645201713406156150827013\\
06371425153796532899526172526614688724212DFBC1B372D89A1188C09C52E0EE\\
C61FCE52032AB1022E8E67ECE6672B043EE5
При этом параметр 
принимает значение:
176866836059344686773017138249002685\\
62746883080675496715288036572431145718978271A4EE429F84EBC423E388964555BB\\
29D3BA53C7BF945E5FAC8F381706354C2
Параметры 
и 
принимают значения:
376991675009019385568410572935126561\\
088413451904919426193045324127437209997595358F8FFB38F7C09ABC782A2DF2A\\
3927DA4077D07205F763682F3A76C9019B4F141719984273434721125159179695007657\\
69246655838972862114499932653333671092213221B4FBBF6D101074EC14AFAC2D4F7\\
EFAC4CF9FEC1ED11BAE336D27D527665
Точка 
имеет координаты:
2970098091581795287437120498393825699\\
042275210799431965163268798205921093339541AA28D2F1AB148280CD9ED56FED\\
A41974053554A42767B83AD043FD39DC04933284253527868466347709466532251708450\\
6804721032454543268132854556539274060910489С375А9941А3049Е33В34361DD\\
204172AD98C3E5916DE27695D22A61FAE46E
Тогда параметр 
принимает значение:
2970098091581795287437120498393825699\\
042275210799431965163268798205921093339541AA28D2F1AB148280CD9ED56FED\\
A41974053554A42767B83AD043FD39DC0493
Поскольку выполнено равенство , то цифровая подпись принимается.
А.2 Пример 2
А.2.1 Параметры схемы цифровой подписи
Для формирования и проверки цифровой подписи должны быть использованы следующие параметры (см. 5.2).
А.2.1.1 Модуль эллиптической кривой
В данном примере параметру присвоено следующее значение:
36239861022290036359077887536838743060213209255346786050\\
8654615045085616662400248258848202227149685402509082360305\\
87351637342638223719649872285829073724034531ACD1FE0023C7550D267B6B2FEE80922B14B2FFB90F04D4EB7C09B5D2D15D\\
F1D852741AF4704A0458047E80E4546D35B8336FAC224DD81664BBF528BE6373
А.2.1.2 Коэффициенты эллиптической кривой
В данном примере параметры a и b принимают следующие значения:
a=7,
a=7,
b=1518655069210828534508950034714043154928747527740206436\\
1940188233528099824437937328297569147859746748660416053978836775\\
96626326413990136959047435811826396
b=1CFF0806A31116DA29D8CFA54E57EB748BC5F377E49400FDD788B649ECA1AC4\\
361834013B2AD7322480A89CA58E0CF74BC9E540C2ADD6897FAD0A3084F302ADC
А.2.1.3 Порядок группы точек эллиптической кривой
В данном примере параметр принимает следующее значение:
36239861022290036359077887536838743060213209255346786050865461\\
50450856166623969164898305032863068499961404079437936585455865192212\\
9707348088126181206197434531ACD1FE0023C7550D267B6B2FEE80922B14B2FFB90F04D4EB7C09B5D2D15D\\
A82F2D7ECB1DBAC719905C5EECC423F1D86E25EDBE23C595D644AAF187E6E6DF
А.2.1.4 Порядок циклической подгруппы группы точек эллиптической кривой
В данном примере параметр принимает следующее значение:
36239861022290036359077887536838743060213209255346786050865461\\
50450856166623969164898305032863068499961404079437936585455865192212\\
9707348088126181206197434531ACD1FE0023C7550D267B6B2FEE80922B14B2FFB90F04D4EB7C09B5D2D15D\\
A82F2D7ECB1DBAC719905C5EECC423F1D86E25EDBE23C595D644AAF187E6E6DF
А.2.1.5 Коэффициенты точки эллиптической кривой
В данном примере координаты точки принимают следующие значения:
19283569440670228493993094012431375989977866354595079743570754913077665\\
9268583544106555768100318487481965800490321233288425233583025072952763238\\
349357327424D19CC64572EE30F396BF6EBBFD7A6C5213B3B3D7057CC825F91093A68CD762\\
FD60611262CD838DC6B60AA7EEE804E28BC849977FAC33B4B530F1B120248A9A22887286933719728599700121555294784163535623273295061803\\
144974259311028603015728141419970722717088070665938506503341523818\\
573477988858648076050987240138542BB312A43BD2CE6E0D020613C857ACDDCFBF061E91E5F2C3F32447C259F39B2\\
C83AB156D77F1496BF7EB3351E1EE4E43DC1A18B91B24640B6DBB92CB1ADD371E
A.2.1.6 Ключ подписи
В данном примере считается, что пользователь обладает следующим ключом подписи .
610081804136373098219538153239847583006845519069531562982388135\\
35489060630178225538360839342337237905766552759511682730702504645883\\
7440766121180466875860BA6048AADAE241BA40936D47756D7C93091A0E8514669700EE7508E508B102072\\
E8123B2200A0563322DAD2827E2714A2636B7BFD18AADFC62967821FA18DD4
А.2.1.7 Ключ проверки подписи
В данном примере считается, что пользователь обладает ключом проверки подписи , координаты которого имеют следующие значения:
9095468530025365965566907686698303100069292725465562815963\\
72965370312498563182320436892870052842808608262832456858223580\\
713780290717986855863433431150561115DC5BC96760C7B48598D8AB9E740D4C4A85A65BE33C1815B5C320C854621D\\
D5A515856D13314AF69BC5B924C8B4DDFF75C45415С1D9DD9DD33612CD530EFE129214572033744256206324497342484154556407008235594887051648958\\
37509539134297327397380287741428246088626609329139441895016863758\\
98410632660057247682237207637C7C90CD40B0F5621DC3AC1В751CFA0E2634FA0503B3D52639F5D7FB72AFD6\\
1ЕА199441D943FFE7F0C70A2759A3CDB84C114E1F9339FDF27F35ECA93677BEEC
А.2.2 Процесс формирования цифровой подписи (алгоритм I)
Пусть после выполнения шагов 1-3 по алгоритму I (см. 6.1) были получены следующие числовые значения:
2897963881682868575562827278553865049173745197871825199562947\\
4190413889509705366611095534999542487330887197488445389646412816544\\
635132969738277062720459643754F3CFACC9E0615C4F4A7C4D8DAB531B09B6F9C170C533A71D147035B0C591\\
7184EE536593F4414339976C647C5D5A407ADEDB1D560C4FC6777D2972075B8C1755163560258504995406282799211252803334510317477377916502\\
081442431820570750344461029867509625089092272358661268724735168078105417\\
47529710309879958632945359E7F4B1410FEACC570456C6801496946312120B39D019D455986E364F3\\
65886748ED7A44B3E794434006011842286212273A6D14CF70EA3AF71BB1AE679F1
При этом кратная точка 
имеет координаты:
24892044770313492650728646430321477536674513192821314440274986373\\
576110928102217951018714129288237168059598287083302842436534530853\\
220044424425341517614622F86FA60A081091A23DD795E1E3C689EE512A3C82EE0DCC2643C78EEA8FCAC\\
D35492558486B20F1С9ЕС197C90699850260C93BCBCD9C5C3317Е19344Е173АЕ3677017388992899183604784479878096044168206263187609613767394680150\\
24422293532765176528442837832456936422662546513702148162933079517\\
08430050152108641508310EB488140F7E2F4E35CF220BDBC75AE44F26F9C7DF52E82436BDE80A91831DA27\\
C8100DAA876F9ADC0D28A82DD3826D4DC7F92E471DA23E55E0EBB3927C85BD6
Параметр 
принимает значение:
24892044770313492650728646430321477536674513192821314440274986373\\
576110928102217951018714129288237168059598287083302842436534530853\\
220044424425341517614622F86FA60A081091A23DD795E1E3C689EE512A3C82EE0DCC2643C78EEA8FCAC\\
D35492558486B20F1С9ЕС197C90699850260C93BCBCD9C5C3317Е19344Е173АЕ36
Параметр 
принимает значение:8645232217076695190388492973829369170750237358484315799195987\\
99313385180564748877195639672460179421760770893278030956807690115\\
822709903853682831835159370,
1081B394696FFE8E6585E7A9362D26B6325F56778AADBC081C0BFBE933D52FF58\\
23CE288E8C4F362526080DF7F70CE406A6EEB1F56919CB92A9853BDE73E5B4A
А.2.3 Процесс проверки цифровой подписи (алгоритм II)
Пусть после выполнения шагов 1-3 по алгоритму II (см. 6.2) было получено следующее числовое значение:
2897963881682868575562827278553865049173745197871825199562947\\
4190413889509705366611095534999542487330887197488445389646412816544\\
63513296973827706272045964,
3754F3CFACC9E0615C4F4A7C4D8DAB531B09B6F9C170C533A71D147035B0C591\\
7184EE536593F4414339976C647C5D5A407ADEDB1D560C4FC6777D2972075B8C
При этом параметр 
принимает значение:
255694215394605222266074084316408615387769223440078319114692849\\
356194345732344708924001925205698280688153534004145821243990606136\\
7072238185934815960252671,
30D212A9E25D1A80A0F238532CADF3E64D7EF4E782B6AD140AAF8BBD9BB4729\\
84595EEC87B2F3448A1999D5F0A6DE0E14A55AD875721EC8CFD504000B3A840FF
Параметры 
и 
принимают значения:
3206470827336768629686907101873475250343306448089030311214484\\
385872743205045180345208826552901003496732941049780357793541942055\\
6000849561981737071979025753D38E7262D69BB2AD24DD81EEA2F92E6348D619FA45007B175837CF13B026079\\
051A48A1A379188F37BA46CE12F7207F2A8345459FF960E1EBD5B4F2A34A6EEF13667709118340031081429778480218475973204553475356412734827\\
320820470283421680060312618142732308792036907264486312226797437575\\
616372669580568058596030082031A18A31602E6EAC0A9888C01941082AEFE296F840453D2603414C2A16EB6FC529\\
D8D8372E50DC49D6C612CE1FF65BD58E1D2029F22690438CC36A76DDA444ACB
Точка 
имеет координаты:
2489204477031349265072864643032147753667451319282131444027498637\\
3576110928102217951018714129288237168059598287083302842436534530853\\
220044424425341517614622F86FA60A081091A23DD795E1E3C689EE512A3C82EE0DCC2643C78EEA8FCAC\\
D35492558486B20F1C9EC197C90699850260C93BCBCD9C5C3317E19344E173AE367701738899289918360478447987809604416820626318760961376739468015\\
0244222935327651765284428378324569364226625465137021481629330795170\\
8430050152108641508310EB488140F7E2F4E35CF220BDBC75AE44F26F9C7DF52E82436BDE80A91831DA27\\
C8100DAA876F9ADC0D28A82DD3826D4DC7F92E471DA23E55E0EBB3927C85BD6
Тогда параметр 
принимает значение:
24892044770313492650728646430321477536674513192821314440274986\\
37357611092810221795101871412928823716805959828708330284243653453085\\
3220044424425341517614622F86FA60A081091A23DD795E1E3C689EE512A3C82EE0DCC2643C78EEA8FCAC\\
D35492558486B20F1C9EC197C90699850260C93BCBCD9C5C3317E19344E173AE36
Поскольку выполнено равенство , то цифровая подпись принимается.
Библиография*
_______________
* Оригиналы международных стандартов ИСО/МЭК находятся в ФГУП "" Федерального агентства по техническому регулированию и метрологии.
[1] | ИСО 2382-2:1976 | Системы обработки информации. Словарь. Часть 2. Арифметические и логические операции |
(ISO 2382-2:1976) | (Data processing - Vocabulary - Part 2: Arithmetic and logic operations) | |
[2] | ИСО/МЭК 9796-2:2010 | Информационные технологии. Методы обеспечения безопасности. Схемы цифровой подписи, обеспечивающие восстановление сообщений. Часть 2. Механизмы на основе целочисленной факторизации |
(ISO/IEC 9796-2:2010) | (Information technology - Security techniques - Digital signature schemes giving message recovery - Part 2: Integer factorization based mechanisms) | |
[3] | ИСО/МЭК 9796-3:2006 | Информационные технологии. Методы обеспечения безопасности. Схемы цифровой подписи, обеспечивающие восстановление сообщений. Часть 3. Механизмы на основе дискретного логарифма |
(ISO/IEC 9796-3:2006) | (Information technology - Security techniques - Digital signature schemes giving message recovery - Part 3: Discrete logarithm based mechanisms) | |
[4] | ИСО/МЭК 14888-1:2008 | Информационные технологии. Методы защиты. Цифровые подписи с приложением. Часть 1. Общие положения |
(ISO/IEC 14888-1:2008) | (Information technology - Security techniques - Digital signatures with appendix - Part 1: General) | |
[5] | ИСО/МЭК 14888-2:2008 | Информационные технологии. Методы защиты. Цифровые подписи с приложением. Часть 2. Механизмы, основанные на разложении на множители |
(ISO/IEC 14888-2:2008) | (Information technology - Security techniques - Digital signatures with appendix - Part 2: Integer factorization based mechanisms) | |
[6] | ИСО/МЭК 14888-3:2006 | Информационные технологии. Методы защиты. Цифровые подписи с приложением. Часть 3. Механизмы на основе дискретного логарифма |
(ISO/IEC 14888-3:2006) | (Information technology - Security techniques - Digital signatures with appendix - Part 3: Discrete logarithm based mechanisms) | |
[7] | ИСО/МЭК 14888-3:2006/ | Информационные технологии. Методы защиты. Цифровые подписи с приложением. Часть 3. Механизмы на основе дискретного логарифма. Изменение 1. Алгоритм русской цифровой подписи эллиптической кривой, алгоритм цифровой подписи Шнора, алгоритм цифровой подписи Шнора для эллиптической кривой и полный алгоритм цифровой подписи Шнора для эллиптической кривой |
(ISO/IEC 14888-3:2006/ | (Information technology - Security techniques - Digital signatures with appendix - Part 3: Discrete logarithm based mechanisms. Ammendment 1. Elliptic Curve Russian Digital Signature Algorithm, Schnorr Digital Signature Algorithm, Elliptic Curve Schnorr Digital Signature Algorithm, and Elliptic Curve Full Schnorr Digital Signature Algorithm) | |
[8] | ИСО/МЭК 10118-1:2000 | Информационные технологии. Методы защиты информации. Хэш-функции. Часть 1. Общие положения |
(ISO/IEC 10118-1:2000) | (Information technology - Security techniques - Hash-functions - Part 1: General) | |
[9] | ИСО/МЭК 10118-2:2010 | Информационные технологии. Методы защиты информации. Хэш-функции. Часть 2. Хэш-функции с использованием алгоритма шифрования |
(ISO/IEC 10118-2:2010) | (Information technology - Security techniques - Hash-functions - Part 2: Hash-functions using an n-bit block cipher) | |
[10] | ИСО/МЭК 10118-3:2004 | Информационные технологии. Методы защиты информации. Хэш-функции. Часть 3. Выделенные хэш-функции |
(ISO/IEC 10118-3:2004) | (Information technology - Security techniques - Hash-functions - Part 3: Dedicated hash-functions) | |
[11] | ИСО/МЭК 10118-4:1998 | Информационные технологии. Методы защиты информации. Хэш-функции. Часть 4. Хэш-функции с применением арифметики в остаточных классах |
(ISO/IEC 10118-4:1998) | (Information technology - Security techniques - Hash-functions - Part 4: Hash-functions using modular arithmetic) |
УДК 681.3.06:006.354 | OKC 35.040 | ОКСТУ 5001 | П85 |
Ключевые слова: обработка данных, передача данных, обмен информацией, сообщения, цифровые подписи, защита информации, формирование цифровой подписи, проверка цифровой подписи | |||
Электронный текст документа
и сверен по:
, 2018
