ГОСТ Р ИСО 10303-513-2009 Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 513. Прикладные интерпретированные конструкции. Элементарное граничное представление

ГОСТ Р ИСО 10303-513-2009

Группа П87

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

Системы автоматизации производства и их интеграция

ПРЕДСТАВЛЕНИЕ ДАННЫХ ОБ ИЗДЕЛИИ И ОБМЕН ЭТИМИ ДАННЫМИ

Часть 513

Прикладные интерпретированные конструкции. Элементарное граничное представление

Industrial automation systems and integration. Product data representation and exchange. Part 513. Application interpreted construct. Elementary boundary representation

ОКС 25.040.40

ОКСТУ 4002

Дата введения 2010-07-01

Предисловие

Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. N 184-ФЗ "О техническом регулировании", а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2001* "Стандартизация в Российской Федерации. Основные положения"

_______________

* Вероятно ошибка оригинала. Следует читать ГОСТ Р 1.0-2004. - .

Сведения о стандарте

1 ПОДГОТОВЛЕН Государственным научным учреждением "Центральный научно-исследовательский и опытно-конструкторский институт робототехники и технической кибернетики" на основе собственного аутентичного перевода на русский язык стандарта, указанного в пункте 4

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 459 "Информационная поддержка жизненного цикла изделий"

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 14 сентября 2009 г. N 367-ст

4 Настоящий стандарт идентичен международному стандарту ИСО 10303-513:2000 "Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 513. Прикладные интерпретированные конструкции. Элементарное граничное представление" (ISO 10303-513:2000 "Industrial automation systems and integration - Product data representation and exchange - Part 513: Application interpreted construct: Elementary boundary representation").

При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты Российской Федерации, сведения о которых приведены в дополнительном приложении ДА

5 ВВЕДЕН ВПЕРВЫЕ

Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе "Национальные стандарты", а текст изменений и поправок - в ежемесячно издаваемых информационных указателях "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет

Введение

Стандарты комплекса ИСО 10303 распространяются на компьютерное представление информации об изделиях и обмен данными об изделиях. Их целью является обеспечение нейтрального механизма, способного описывать изделия на всем протяжении их жизненного цикла. Этот механизм применим не только для обмена файлами в нейтральном формате, но является также основой для реализации и совместного доступа к базам данных об изделиях и организации архивирования.

Стандарты комплекса ИСО 10303 представляют собой набор отдельно издаваемых стандартов (частей). Стандарты данного комплекса относятся к одной из следующих тематических групп: "Методы описания", "Методы реализации", "Методология и основы аттестационного тестирования", "Интегрированные обобщенные ресурсы", "Интегрированные прикладные ресурсы", "Прикладные протоколы", "Комплекты абстрактных тестов", "Прикладные интерпретированные конструкции" и "Прикладные модули". Настоящий стандарт входит в группу "Прикладные интерпретированные конструкции".

Прикладная интерпретированная конструкция (ПИК) обеспечивает логическую группировку интерпретированных конструкций, поддерживающих конкретную функциональность для использования данных об изделии в разнообразных прикладных контекстах. Интерпретированная конструкция представляет собой обычную интерпретацию интегрированных ресурсов, поддерживающую требования совместного использования информации прикладными протоколами.

Настоящий стандарт определяет прикладную интерпретированную конструкцию для определения граничного представления твердого тела с элементарной геометрией и явной топологией.

1 Область применения

Настоящий стандарт определяет интерпретацию обобщенных ресурсов, обеспечивающую соответствие требованиям к определению модели элементарного граничного представления.

Требования настоящего стандарта распространяются на:

- определение объекта elementary_brep_shape_representation, являющегося представлением, образованным одним или несколькими объектами manifold_solid_brep, каждый из которых определен элементарной геометрией и полностью явной топологией;

- определение неограниченной геометрии кривых и поверхностей, используемых для определения граней В-rep модели;

- определение топологической структуры В-rep модели;

- трехмерную геометрию;

- В-rep модели (модели граничного представления);

- элементарные кривые, представляемые объектами line и conic;

- объекты elementary_surface;

- геометрические преобразования;

- объекты polyline;

- неограниченную геометрию;

- использование топологии для ограничения геометрических объектов.

Требования настоящего стандарта не распространяются на:

- двумерную геометрию;

- ограниченные кривые, кроме объектов polyline;

- ограниченные поверхности;

- смещенные кривые и поверхности.

ПИК, определенная настоящим стандартом, не зависит от какой-либо промышленной прикладной области.

2 Нормативные ссылки

В настоящем стандарте использованы ссылки на следующие международные стандарты:

ИСО/МЭК 8824-1:1995 Информационные технологии. Взаимосвязь открытых систем. Абстрактная синтаксическая нотация версии один (АСН.1). Часть 1. Спецификация основной нотации (ISO/IEC 8824-1:1995, Information technology - Abstract Syntax Notation One (ASN.1): Specification of basic notation)

ИСО 10303-1:1994 Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 1. Общие представления и основополагающие принципы (ISO 10303-1:1994, Industrial automation systems and integration - Product data representation and exchange - Part 1: Overview and fundamental principles)

ИСО 10303-11:1994 Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 11. Методы описания. Справочное руководство по языку EXPRESS (ISO 10303-11:2004, Industrial automation systems and integration - Product data representation and exchange - Part 11: Description methods: The EXPRESS language reference manual)

ИСО/ТО 10303-12:1997 Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 12. Методы описания. Справочное руководство по языку EXPRESS-I (ISO/TR 10303-12:1997, Industrial automation systems and integration - Product data representation and exchange - Part 12: Description methods: The EXPRESS-I language reference manual)

ИСО 10303-41:1994 Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 41. Интегрированные обобщенные ресурсы. Основы описания и поддержки изделий (ISO 10303-41:1994, Industrial automation systems and integration - Product data representation and exchange - Part 41: Integrated generic resource: Fundamentals of product description and support)

ИСО 10303-42:1994 Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 42. Интегрированные обобщенные ресурсы. Геометрическое и топологическое представление (ISO 10303-42:2003, Industrial automation systems and integration - Product data representation and exchange - Part 42: Integrated generic resource: Geometric and topological representation)

ИСО 10303-43:1994 Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 43. Интегрированные обобщенные ресурсы. Структуры представлений (ISO 10303-43:1994, Industrial automation systems and integration - Product data representation and exchange - Part 43: Integrated generic resources: Representation structures)

ИСО 10303-202:1996 Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 202. Прикладные протоколы. Ассоциативные чертежи (ISO 10303-202:1996, Industrial automation systems and integration - Product data representation and exchange - Part 202: Application protocol: Associative draughting)

ИСО 10303-514:1999 Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 514. Прикладные интерпретированные конструкции. Расширенное граничное представление (ISO 10303-514:1999, Industrial automation systems and integration - Product data representation and exchange - Part 514: Application interpreted construct: Advanced boundary representation)

3 Термины и определения

3.1 Термины, определенные в ИСО 10303-1

В настоящем стандарте применены следующие термины:

- приложение (application);

- прикладной контекст (application context);

- прикладной протокол; ПП (application protocol; АР);

- метод реализации (implementation method);

- интегрированный ресурс (integrated resource);

- интерпретация (interpretation);

- данные об изделии (product data).

3.2 Термины, определенные в ИСО 10303-42

В настоящем стандарте применены следующие термины:

- линейно связный (arcwise connected);

- граница (boundary);

- ограничения (bounds);

- координатное пространство (coordinate space);

- кривая (curve);

- незамкнутая кривая (open curve);

- ориентируемый (orientable);

- поверхность (surface);

- топологическое значение (topological sense).

3.3 Термин, определенный в ИСО 10303-202

В настоящем стандарте применен следующий термин:

прикладная интерпретированная конструкция (ПИК) (application interpreted construct; AIC).

3.4 Термин, определенный в ИСО 10303-514

В настоящем стандарте применен следующий термин:

односвязное твердое тело (manifold solid).

3.5 Другие определения

В настоящем стандарте также применены следующие термины с соответствующими определениями:

3.5.1 представление формы элементарными В-rep моделями (elementary B-rep shape representation): Представление формы, состоящее из одной или более В-rep моделей односвязных твердых тел. Каждая составляющая В-rep модели должна иметь грани и ребра, определенные посредством элементарной геометрии.

3.5.2 элементарная геометрия (elementary geometry): Геометрия, образованная линиями, полилиниями, линиями второго порядка и элементарными поверхностями.

4 Сокращенный листинг на языке EXPRESS

В настоящем разделе определена EXPRESS-схема, в которой используются элементы интегрированных ресурсов и содержатся типы, конкретизации объектов и функции, относящиеся к настоящему стандарту.

Примечание - В интегрированных ресурсах допускается существование подтипов и элементов списков выбора, не импортированных в данную ПИК. Такие конструкции исключают из дерева подтипов или из списка выбора посредством правил неявного интерфейса, определенных в ИСО 10303-11. Ссылки на исключенные конструкции находятся вне области применения данной ПИК. В некоторых случаях исключаются все элементы списка выбора. Поскольку ПИК предназначены для реализации в контексте прикладного протокола, элементы списка выбора будут определяться областью применения прикладного протокола.

Данная прикладная интерпретированная конструкция предоставляет непротиворечивое множество геометрических и топологических объектов для определения моделей односвязных твердых тел с гранями, имеющими элементарную геометрию и явно определенными ребрами и вершинами. Грани В-rep моделей ограничены полилиниями, линиями или кривыми второго порядка.

Объектом самого верхнего уровня в данной ПИК является объект elementary_brep_shape_representation. Этот объект является конкретизацией объекта shape_representation (см. ИСО 10303-41), состоящей из объектов manifold_solid_brep и mapped_item, определенных как поступательно перемещенные или преобразованные копии объектов manifold_solid_brep с элементарной геометрией.

EXPRESS-спецификация

Примечания

1 Для объекта connected_face_set установлены явные интерфейсы (т.е. они включены в списки оператора USE FROM), чтобы разрешить правилам, определенным для объекта elementary_brep_shape_representation, доступ к атрибутам этого объекта. При использовании данной ПИК данный объект должен быть реализован в виде одного из своих подтипов.

2 Схемы, на которые выше даны ссылки, можно найти в следующих стандартах комплекса ИСО 10303:

4.1 Основные понятия и допущения

Для независимой реализации в схемах прикладных протоколов, использующих данную ПИК, предназначены следующие объекты:

- axis2_placement_3d;

- brep_with_voids;

- cartesian_point;

- cartesian_transformation_operator_3d;

- circle;

- closed_shell;

- conical_surface;

- cylindrical_surface;

- degenerate_toroidal_surface;

- direction;

- edge_curve;

- edge_loop;

- elementary_face;

- ellipse;

- face_bound;

- face_outer_bound;

- face_surface;

- hyperbola;

- line;

- manifold_solid_brep;

- mapped_item;

- oriented_closed_shell;

- parabola;

- plane;

- polyline;

- representation_map;

- spherical_surface;

- toroidal_surface;

- vector;

- vertex_loop;

- vertex_point.

Прикладной протокол, использующий данную ПИК, должен обеспечивать поддержку всех вышеперечисленных объектов.

Прикладной протокол, использующий данную ПИК, должен допускать реализацию объекта shape_representation как объекта elementary_brep_shape_representation.

4.2 Определения объекта elementary_brep_shape_representation схемы aic_elementary_ brep

Объект elementary_brep_shape_representation является подтипом объекта shape_representation, в котором элементы представления являются конкретизациями объектов manifold_solid_brep. Эти конкретизации отличаются от более общей В-rep модели тем, что для представления граней и ребер используются только явные геометрические формы. Геометрия граней ограничена объектами elementary_surface и линиями ребер, которые могут быть представлены объектами line, polyline или conic.

Формальные утверждения

WR1 - атрибут items, супертипа representation должен содержать только объекты manifold_solid_brep, mapped_item и axis2_placement_3d. Согласно этому правилу, использование объектов faceted_brep недопустимо, поскольку экземпляр объекта faceted_brep также имел бы тип manifold_solid_brep.

WR2 - по крайней мере один элемент из множества элементов items должен быть объектом manifold_solid_brep или mapped_item (см. также WR11).

WR3 - Все грани, используемые для построения объекта manifold_solid_brep должны иметь тип face_surface.

Примечание - Вызов функции msb_shells в WR3 и последующих утверждениях является корректным, так как, хотя обобщенным типом аргумента 'msb' является representation_item, но оператором QUERY для него был определен тип manifold_solid_brep.

WR4 - для каждого объекта manifold_solid_brep из множества элементов items, ассоциированная поверхность для каждой грани должна быть объектом elementary_surface.

WR5 - для каждого объекта manifold_solid_brep из множества элементов items, ребра, используемые для определения границ, должны иметь тип edge_curve.

WR6 - для каждого объекта manifold_solid_brep из множества элементов items, каждая кривая, используемая для определения ограничений граней, должна быть объектом conic, line или polyline.

WR7 - для каждого объекта manifold_solid_brep из множества элементов items, все ребра, используемые для определения границ, должны быть обрезаны вершинами, имеющими тип vertex_point.

WR8 - для каждого объекта manifold_solid_brep из множества элементов items, каждый объект polyline, используемый для определения части ограничений грани, должен содержать три или более точек.

WR9 - для каждого объекта manifold_solid_brep из множества элементов items, атрибут внешней оболочки не должен иметь тип oriented_closed_shell.

WR10 - если объект brep_with_voids включены в множество элементов items, то каждая оболочка в множестве voids должна быть объектом oriented_closed_shell со значением ориентации FALSE.

WR11 - если объект mapped_item включен в множество элементов items, то объект mapped_representation атрибута mapping_source должен быть объектом elementary_brep_shape_representation.

Примечание - Если объект cartesian_transformation_operator_3d включен как объект mapped_item.mapping_target с объектом axis2_placement_3d, который соответствует в исходной системе координат объекту mapped_representation.mapping_origin, то результирующий объект mapped_item является преобразованной копией объекта elementary_brep_shape_representation. Точное определение данного преобразования, включая поступательное перемещение, вращение, масштабирование и, при необходимости, зеркалирование, задается оператором преобразования.

WR12 - для каждого объекта manifold_solid_brep из множества элементов items любой объект vertex_loop, используемый для определения ограничения грани, должен ссылаться на объект vertex_point с геометрией, определяемой объектом cartesian_point.

Приложение А
(обязательное)

Сокращенное наименование объекта

Сокращенное наименование объекта, установленного в настоящем стандарте, приведено в таблице А.1. Требования к использованию сокращенных наименований объектов содержатся в стандартах тематической группы "Методы реализации" комплекса ИСО 10303.

Таблица А.1 - Сокращенное наименование объекта

Приложение В
(обязательное)

Регистрация информационного объекта

В.1 Обозначение документа

Для обеспечения однозначного обозначения информационного объекта в открытой системе настоящему стандарту присвоен следующий идентификатор объекта:

{ iso standard 10303 part(513) version(1) }

Смысл данного обозначения установлен в ИСО/МЭК 8824-1 и описан в ИСО 10303-1.

В.2 Обозначение схемы

Для обеспечения однозначного обозначения в открытой информационной системе схеме aic_elementary_brep (см. раздел 4) присвоен следующий идентификатор объекта:

{ iso standard 10303 part(513) version(1) object(1) aic-elementary-brep(1) }

Смысл данного обозначения установлен в ИСО/МЭК 8824-1 и описан в ИСО 10303-1.

Приложение С
(справочное)

Машинно-интерпретируемые листинги

В данном приложении приведены ссылки на сайты, на которых находятся листинги наименований объектов на языке EXPRESS и соответствующих сокращенных наименований, установленных в настоящем стандарте. На этих же сайтах находятся листинги всех EXPRESS-схем, установленных или на которые даются ссылки в настоящем стандарте, без комментариев и другого поясняющего текста. Эти листинги доступны в машинно-интерпретируемой форме и могут быть получены по следующим адресам URL:

Сокращенные наименования: //www.mel.nist.gov/div826/subject/apde/snr/

EXPRESS: //www.mel.nist.gov/step/parts/part513/is/

При невозможности доступа к этим сайтам, необходимо обратиться в центральный секретариат ИСО или непосредственно в секретариат ИСО ТК184/ПК4 по адресу электронной почты: [email protected].

Примечание - Информация, представленная в машинно-интерпретируемой форме по указанным выше адресам URL, является справочной. Обязательным является текст настоящего стандарта.

Приложение D
(справочное)

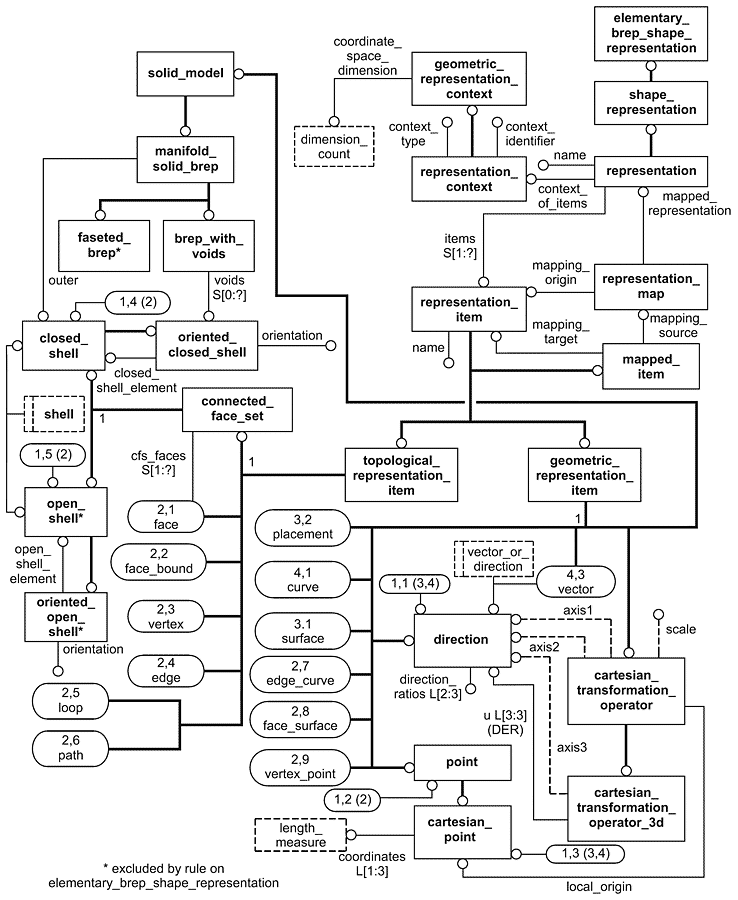
EXPRESS-G диаграммы

Диаграммы, приведенные на рисунках D.1-D.4 получены из сокращенного листинга ПЭМ на языке EXPRESS, определенного в разделе 4. В диаграммах использована графическая нотация EXPRESS-G языка EXPRESS. Описание EXPRESS-G установлено в ИСО 10303-11, приложение D.

Примечания

1 Приведенные ниже выбранные типы импортируются в расширенный листинг ПИК в соответствии с правилами неявных интерфейсов по ИСО 10303-11. В настоящем стандарте эти выбранные типы в других объектах не используются:

- geometric_set_select;

- pcurve_or_surface;

- reversible_topology;

- shell;

- trimming_select;

- vector_or_direction.

2 Правила неявных интерфейсов, определенные в ИСО 10303-11, вводят также некоторые объекты, реализация которых запрещена правилами, относящимися к объекту elementary_brep_shape_representation. Эти объекты отмечены на EXPRESS-G диаграммах символом "*".

Рисунок D.1 - ПИК elementary_boundary_representation в формате EXPRESS-G (диаграмма 1 из 4)

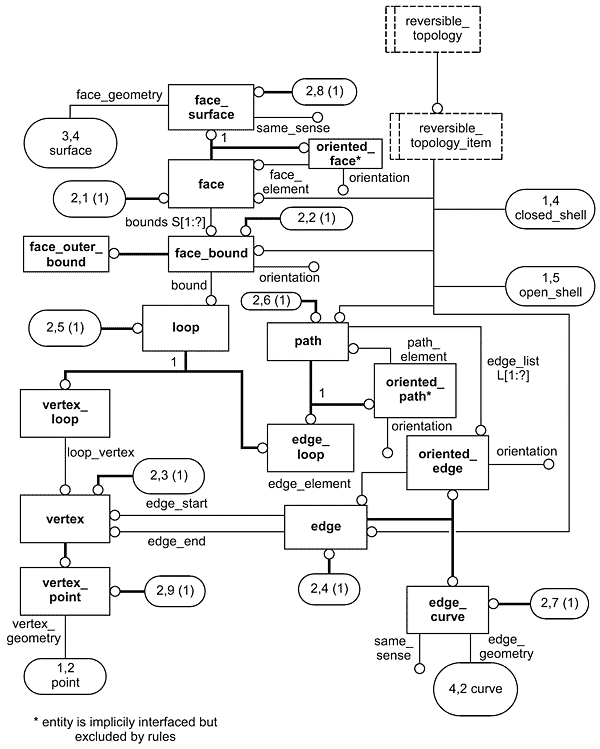
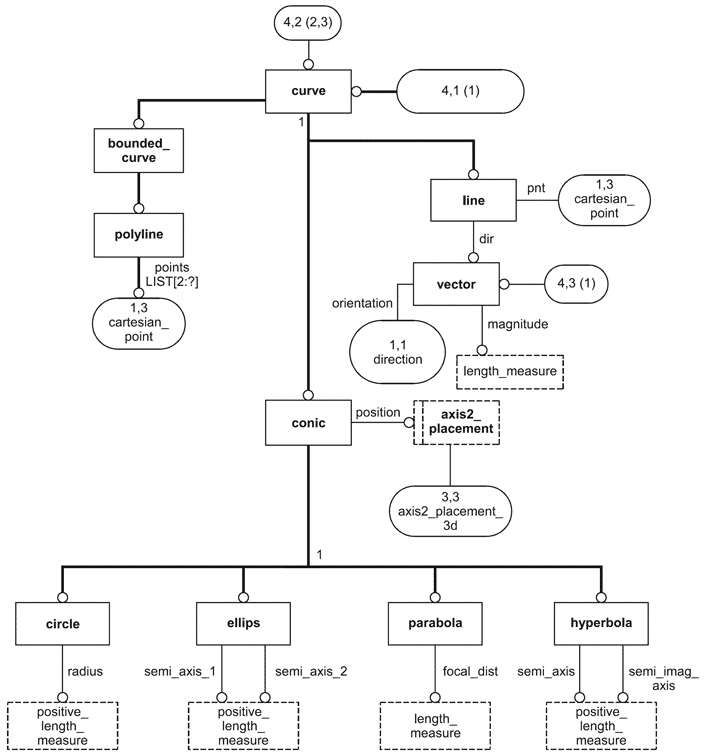
Рисунок D.2 - ПИК elementary_boundary_representation в формате EXPRESS-G (диаграмма 2 из 4)

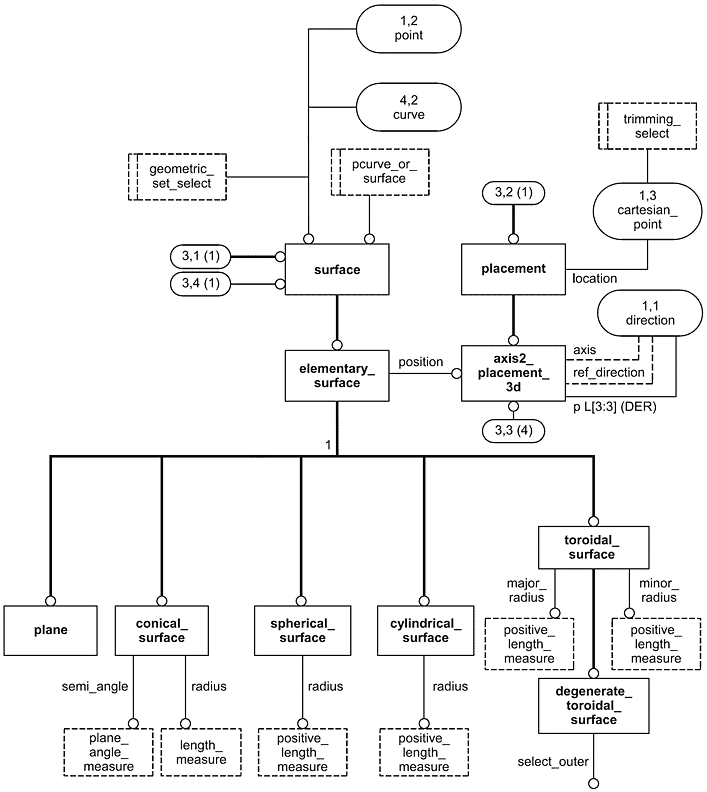
Рисунок D.3 - ПИК elementary_boundary_representation в формате EXPRESS-G (диаграмма 3 из 4)

Рисунок D.4 - ПИК elementary_boundary_representation в формате EXPRESS-G (диаграмма 4 из 4)

Приложение Е
(справочное)

Требования соответствия и цели тестирования ПИК

Е.1 Требования соответствия ПИК: элементарная В-rep модель

Любой прикладной протокол, использующий данную ПИК, может потребовать согласования с определенными ниже требованиями соответствия ПИК при реализации объекта elementary_brep_shape_representation.

Соответствие данной ПИК означает, что должны поддерживаться все типы данных и типы объектов, определенные в листинге на языке EXPRESS. Единственным допустимым использованием экземпляра геометрического или топологического объекта в контексте данной ПИК является его использование для определения объекта elementary_brep_shape_representation.

Указанные ниже объекты могут быть реализованы как часть определения объекта elementary_brep_shape_representation:

- axis2_placement_3d;

- brep_with_voids;

- cartesian_point;

- cartesian_transformation_operator_3d;

- circle;

- closed_shell;

- conical_surface;

- cylindrical_surface;

- degenerate_toroidal_surface;

- direction;

- edge_curve;

- edge_loop;

- elementary_face;

- ellipse;

- face_bound;

- face_outer_bound;

- face_surface;

- hyperbola;

- line;

- manifold_solid_brep;

- mapped_item;

- oriented_closed_shell;

- parabola;

- plane;

- polyline;

- representation_map;

- spherical_surface;

- toroidal_surface;

- vector;

- vertex_loop;

- vertex_point.

E.2 Цели тестирования ПИК элементарной В-rep модели

В настоящем разделе определены цели тестирования для ПИК элементарной В-rep модели. Цели тестирования основаны на конструкциях, определенных в разделе 4.

E.2.1 Объект elementary_brep_shape_representation

На основании определения данного объекта сформулированы следующие цели тестирования:

ЕВ1 - проверка объекта representation как объекта shape_representation и как объекта elementary_brep_shape_representation (см. E.3.1).

ЕВ2 - проверка объекта elementary_brep_shape_representation с атрибутом context, представленным как объект geometric_context с атрибутом items, представленным как объект manifold_solid_brep (см. Е.3.1).

ЕВ3 - проверка объекта elementary_brep_shape_representation с атрибутом context, представленным как объект geometric_context с атрибутом items, представленным как объект mapped_item (см. Е.3.6).

ЕВ4 - проверка объекта elementary_brep_shape_representation с атрибутом context, представленным как объект geometric_context с атрибутом items, представленным двумя или более элементами, представленными как объекты manifold_solid_brep, или mapped_item, или axis2_placement_3d. При этом по меньшей мере один из них должен быть объектом axis2_placement_3d (см. Е.3.6).

E.2.2 Объект manifold_solid_brep

На основании определения данного объекта сформулированы следующие цели тестирования:

ЕВ5 - проверка объекта manifold_solid_brep с атрибутом outer (атрибут voids отсутствует), представленным как объект closed_shell (но не как подтип oriented_closed_shell) (см. Е.3.1).

ЕВ6 - проверка объекта manifold_solid_brep как подтипа brep_with_voids с атрибутом outer, представленным как объект closed_shell, и атрибутом voids, представленным множеством, состоящим из одного объекта oriented_closed_shell (атрибут voids присутствует) (см. Е.3.2).

ЕВ7 - проверка объекта manifold_solid_brep как подтипа brep_with_voids с атрибутом outer, представленным кaк oбъeкт closed_shell, и атрибутом voids, представленным множеством, состоящим из более чем одного объекта oriented_closed_shell (атрибут voids присутствует) (см. Е.3.2).

E.2.3 Объект oriented_closed_shell

На основании определения данного объекта и ограничений, наложенных на объект elementary_brep_shape_representation, сформулирована следующая цель тестирования:

ЕВ8 - проверка объекта oriented_closed_shell с атрибутом orientation, имеющим значение FALSE (см. E.3.2).

E.2.4 Объект closed_shell

На основании определения данного объекта и ограничений, наложенных на объект elementary_brep_shape_representation, сформулированы следующие цели тестирования:

ЕВ9 - проверка объекта closed_shell с атрибутом cfs_faces, представленным множеством, состоящим из одного объекта face_surface (см. E.3.2).

ЕВ10 - проверка объекта closed_shell с атрибутом cfs_faces, представленным множеством, состоящим из более чем одного объекта face_surface (см. Е.3.1).

Е.2.5 Объект face

На основании определения данного объекта и ограничений, наложенных на объект elementary_brep_shape_representation, сформулированы следующие цели тестирования:

ЕВ11 - проверка объекта face как объекта face_surface с атрибутом bounds, представленным множеством, состоящим из одного объекта face_bound, представленного как объект face_outer_bound с атрибутом orientation, имеющим значение TRUE (см. Е.3.1).

ЕВ12 - проверка объекта face как объекта face_surface с атрибутом bounds, представленным множеством, состоящим из одного объекта face_bound, представленного как объект face_outer_bound с атрибутом bound, представленным объектом edge_loop (но не oriented_path) и атрибутом orientation, имеющим значение FALSE (см. E.3.1).

ЕВ13 - проверка объекта face как объекта face_surface с атрибутом bounds, представленным множеством, состоящим, по меньшей мере, из двух объектов face_bound с атрибутом bound, представленным объектом edge_loop и атрибутом orientation, имеющим значение TRUE (см. Е.3.1).

ЕВ14 - проверка объекта face как объекта face_surface с атрибутом bounds, представленным множеством, состоящим, по меньшей мере, из двух объектов face_bound с атрибутом bound, представленным объектом edge_loop и атрибутом orientation, имеющим значение FALSE (см. Е.3.1).

ЕВ15 - проверка объекта face как объекта face_surface с атрибутом bounds, представленным множеством, состоящим, по меньшей мере, из двух объектов face_bound (включая один объект vertex_loop) (см. Е.3.5).

E.2.6 Объект face_surface

На основании определения данного объекта и ограничений, наложенных на объект elementary_brep_shape_representation, сформулированы следующие цели тестирования:

ЕВ16 - проверка объекта face_surface с атрибутом face_geometry, представленным как объект surface (см. E.3.1).

ЕВ17 - проверка объекта face_surface с атрибутом same_sense, имеющим значение TRUE (см. Е.3.1).

ЕВ18 - проверка объекта face_surface с атрибутом same_sense, имеющим значение FALSE (см. Е.3.5).

E.2.7 Объект surface

На основании определения данного объекта и ограничений, наложенных на объект face_surface, сформулирована следующая цель тестирования:

ЕВ19 - проверка объекта surface как объекта elementary_surface (см. Е.3.1).

E.2.8 Объект elementary_surface

На основании определения данного объекта и ограничений, наложенных на объект face_surface, сформулированы следующие цели тестирования:

ЕВ20 - проверка объекта elementary_surface с атрибутом position, представленным как объект axis2_placement_3d с присутствием атрибута axis (см. Е.3.1).

ЕВ21 - проверка объекта elementary_surface с атрибутом position, представленным как объект axis2_placement_3d с отсутствием атрибута axis (см. Е.3.4).

ЕВ22 - проверка объекта elementary_surface с атрибутом position, представленным как объект axis2_placement_3d с присутствием атрибута ref_direction (см. Е.3.1).

ЕВ23 - проверка объекта elementary_surface с атрибутом position, представленным как объект axis2_placement_3d с отсутствием атрибута ref_direction (см. Е.3.4).

ЕВ24 - проверка объекта elementary_surface как объекта plane (см. Е.3.1).

ЕВ25 - проверка объекта elementary_surface как объекта cylindrical_surface (см. Е.3.1).

ЕВ26 - проверка объекта elementary_surface как объекта conical_surface (см. Е.3.5).

ЕВ27 - проверка объекта elementary_surface как объекта spherical_surface (см. Е.3.1).

ЕВ28 - проверка объекта elementary_surface как объекта toroidal_surface (см. Е.3.3).

Е.2.9 Объект loop

На основании определения данного объекта и ограничений, наложенных на объект face_surface, сформулированы следующие цели тестирования:

ЕВ29 - проверка объекта loop как объекта edge_loop (см. Е.3.1).

ЕВ30 - проверка объекта loop как объекта vertex_loop с атрибутом loop_vertex, представленным как объект vertex_point с атрибутом vertex_geometry, представленным как объект cartesian_point (см. Е.3.2).

E.2.10 Объект edge

На основании определения данного объекта и ограничений, наложенных на объект face_surface, сформулированы следующие цели тестирования:

ЕВ31 - проверка объекта edge как объекта edge_curve с атрибутами edge_start и edge_end, представленными объектом vertex_point (см.E.3.1).

ЕВ32 - проверка объекта edge как объекта oriented_edge с атрибутом orientation, имеющим значение TRUE (см. E.3.1).

ЕВ33 - проверка объекта edge как объекта oriented_edge с атрибутом orientation, имеющим значение FALSE (см. E.3.3).

E.2.11 Объект edge_curve

На основании определения данного объекта и ограничений, наложенных на объект face_surface, сформулированы следующие цели тестирования:

ЕВ34 - проверка объекта edge_curve с атрибутом edge_geometry, представленным как объект line (см. E.3.3).

ЕВ35 - проверка объекта edge_curve с атрибутом edge_geometry, представленным как объект polyline (см. E.3.4).

ЕВ36 - проверка объекта edge_curve с атрибутом edge_geometry, представленным как объект conic (см. E.3.1).

ЕВ37 - проверка объекта edge_curve с атрибутом same_sense, имеющим значение TRUE (см. Е.3.1).

ЕВ38 - проверка объекта edge_curve с атрибутом same_sense, имеющим значение FALSE (см. Е.3.5).

E.2.12 Объект conic

На основании определения данного объекта и ограничений, наложенных на объект face_surface, сформулированы следующие цели тестирования:

ЕВ39 - проверка объекта conic как объекта circle (см. Е.3.1).

ЕВ40 - проверка объекта conic как объекта ellipse (см. Е.3.1).

ЕВ41 - проверка объекта conic как объекта hyperbola (см. Е.3.5).

ЕВ42 - проверка объекта conic как объекта parabola (см. Е.3.5).

E.2.13 Объект polyline

На основании определения данного объекта и ограничений, наложенных на объект face_surface, сформулирована следующая цель тестирования:

ЕВ43 - проверка объекта polyline с атрибутом points, представленным списком из трех или более объектов cartesian_point (см. E.3.4).

E.2.14 Объект cartesian_transformation_operator_3d

На основании определения данного объекта, объекта mapped_item и ограничений, наложенных на объект elementary_brep_shape_representation, сформулированы следующие цели тестирования:

ЕВ44 - проверка объекта mapped_item с атрибутом mapping_target, представленным как объект cartesian_transformation_operator_3d (см. E.3.7).

EB45 - проверка объекта cartesian_transformation_operator как объекта cartesian_transformation_operator_3d с масштабом, представленным значением типа REAL, не равным 1,0 (см. Е.3.7).

Е.3 Абстрактные контрольные примеры для модели элементарного граничного представления

Абстрактные контрольные примеры для постпроцессора представлены в настоящем разделе на языке EXPRESS-I.

Для каждого контрольного примера для препроцессора приведено простое текстовое описание, чтобы обеспечить возможность создания модели, подобной той, которая представлена на языке EXPRESS-I для тестирования постпроцессора. Для каждого контрольного примера определен ряд относящихся к нему целей тестирования.

Примечание - Многие из целей тестирования применимы к нескольким контрольным примерам, но критерии определены только для первого из них. В частности, это относится ко многим целям, приведенным в контрольном примере eb1.

Е.3.1 Контрольный пример eb1

Контрольный пример eb1 является наиболее фундаментальным контрольным примером, описывающим грани, необходимые для определения одиночного сплошного цилиндра с полусферическим основанием и эллиптической верхней гранью. Вся геометрия задана в явной форме без значений, принимаемых по умолчанию, и без необходимости изменения направлений на обратные. Определение граней обеспечивается контекстом объекта cylinder_sphere_shell с использованием исходных параметров.

Е.3.1.1 Цели тестирования

Ниже перечислены цели тестирования прикладной интерпретированной модели, охватываемые данным контрольным примером.

ЕВ1 - проверка объекта representation как объекта shape_representation и как объекта elementary_brep_shape_representation.

ЕВ2 - проверка объекта elementary_brep_shape_representation с атрибутом context, представленным как объект geometric_representation_context с атрибутом items, представленным как объект manifold_solid_brep.

ЕВ5 - проверка объекта manifold_solid_brep с атрибутом outer (атрибут voids отсутствует), представленным как объект closed_shell (но не как подтип oriented_closed_shell).

ЕВ10 - проверка объекта closed_shell с атрибутом cfs_faces, представленным множеством, состоящим из более чем одного объекта face_surface.

ЕВ11 - проверка объекта face как объекта face_surface с атрибутом bounds, представленным множеством, состоящим из одного объекта face_bound, представленного как объект face_outer_bound с атрибутом orientation, имеющим значение TRUE.

ЕВ12 - проверка объекта face как объекта face_surface с атрибутом bounds, представленным множеством, состоящим из одного объекта face_bound, представленного как объект face_outer_bound с атрибутом orientation, имеющим значение FALSE.

ЕВ13 - проверка объекта face как объекта face_surface с атрибутом bounds, представленным множеством, состоящим, по меньшей мере, из двух объектов face_bound с атрибутом bound, представленным объектом edge_loop и атрибутом orientation, имеющим значение TRUE.

ЕВ14 - проверка объекта face как объекта face_surface с атрибутом bounds, представленным множеством, состоящим, по меньшей мере, из двух объектов face_bound с атрибутом bound, представленным объектом edge_loop и атрибутом orientation, имеющим значение FALSE.

ЕВ16 - проверка объекта face_surface с атрибутом face_geometry, представленным как объект surface.

ЕВ17 - проверка объекта face_surface с атрибутом same_sense, имеющим значение TRUE.

ЕВ19 - проверка объекта surface как объекта elementary_surface.

ЕВ20 - проверка объекта elementary_surface с атрибутом position, представленным как объект axis2_placement_3d с присутствием атрибута axis.

ЕВ22 - проверка объекта elementary_surface с атрибутом position, представленным как объект axis2_placement_3d с присутствием атрибута ref_direction.

ЕВ24 - проверка объекта elementary_surface как объекта plane.

ЕВ25 - проверка объекта elementary _surface как объекта cylindrical_surface.

ЕВ27 - проверка объекта elementary _surface как объекта spherical_surface.

ЕВ29 - проверка объекта loop как объекта edge_loop.

ЕВ31 - проверка объекта edge как объекта edge_curve с атрибутами edge_start и edge_end, представленными объектом vertex_point.

ЕВ32 - проверка объекта edge как объекта oriented_edge с атрибутом orientation, имеющим значение TRUE.

ЕВ36 - проверка объекта edge_curve с атрибутом edge_geometry, представленным как объект conic.

ЕВ37 - проверка объекта edge_curve с атрибутом same_sense, имеющим значение TRUE.

ЕВ39 - проверка объекта conic как объекта circle.

ЕВ40 - проверка объекта conic как объекта ellipse.

Е.3.1.2 Спецификация входа в препроцессор

Создается объект elementary_brep_shape_representation, состоящий из единственного объекта manifold_solid_brep. Объект manifold_solid_brep должен иметь форму сплошного цилиндра с полусферическим основанием и плоской наклонной верхней гранью. Центр полусферы находится в начале координат, а ось Z является осью цилиндра. В-rep модель представлена одной замкнутой оболочкой с тремя гранями. Соответствующее множество размеров определено в приведенной ниже спецификации на языке EXPRESS-I.

Примечание - Для определения граней В-rep модели использован контекст объекта cylinder_sphere_shell в своей простейшей форме с параметрами, заданными по умолчанию.

Е.3.1.3 Спецификация входа в постпроцессор

E.3.1.4 Критерии решения постпроцессора

EB1 - все формальные утверждения для объекта elementary_brep_shape_representation должны быть проверены.

ЕВ2 - единицы длины должны быть правильно интерпретированы, воссозданная модель не должна содержать объекты polyloop или vertex_loop.

ЕВ5 - перпендикуляры к оболочке должны быть направлены от нее.

ЕВ10 - грани должны быть соединены вдоль ребер, другие пересечения граней недопустимы.

ЕВ11 - геометрия граней должна быть правильно обрезана объектом face_bound.

ЕВ12 - объекты face_bound с значением атрибута orientation FALSE должны быть правильно интерпретированы, чтобы определить правильную часть поверхности грани.

ЕВ13 - Множество ограничений должно быть правильно обработано, чтобы обрезать грань.

ЕВ14 - объекты face_bound с разными значениями атрибута orientation должны быть правильно интерпретированы.

ЕВ16 - объекты edge_curve и вершины, ограничивающие объекты edge_loop, должны лежать на поверхности, определяющей объект face_geometry.

ЕВ20 - объект axis2_placement с атрибутом axis должен быть правильно интерпретирован, чтобы определить положение поверхности.

ЕВ22 - объект axis2_placement с атрибутом ref_direction должен быть правильно интерпретирован, чтобы определить положение поверхности.

ЕВ24 - ограничивающие контуры грани с объектом face_geometry, представленным как объект plane, должны быть копланарны.

ЕВ25 - неограниченный объект cylindrical_surface должен быть ограничен объектами edge_loop.

ЕВ27 - правильная часть объекта spherical_surface должна быть определена объектами edge_loop.

ЕВ31 - все объекты vertex_point должны принадлежать объектам edge_curve.

ЕВ36 - объект edge с идентичными начальной и конечной вершинами и объект edge_geometry, представленный эллипсом, должны быть правильно интерпретированы как замкнутый эллипс.

ЕВ39 - объект edge с идентичными начальной и конечной вершинами и объект edge_geometry, представленный окружностью, должны быть правильно интерпретированы как замкнутая окружность.

ЕВ40 - подтип ellipse объекта conic должен быть правильно интерпретирован.

Е.3.2 Контрольный пример eb2

Контрольный пример еb2 разработан для проверки определения элементарного граничного представления, содержащего одну или несколько пустот. Контекст объекта cylinder_sphere_shell используется с различными параметрами для определения внешней оболочки и оболочек пустот. Результатом является полый сплошной цилиндр с расположенной внутри пустотой (или пустотами) той же или сферической формы.

Примечание - При необходимости данный тест может быть легко модифицирован для проверки геометрической точности путем изменения параметров, определяющих пустоты, расположенных очень близко друг к другу или к внешней оболочке. В текущей версии данного контрольного примера возможность такого вмешательства не предусмотрена.

Е.3.2.1 Цели тестирования

Ниже перечислены цели тестирования, охватываемые данным контрольным примером.

ЕВ6 - проверка объекта manifold_solid_brep как подтипа brep_with_voids с атрибутом outer, представленным как объект closed_shell, и атрибутом voids, представленным множеством, состоящим из одного объекта oriented_closed_shell (атрибут voids присутствует).

ЕВ7 - проверка объекта manifold_solid_brep как подтипа brep_with_voids с атрибутом outer, представленным как объект closed_shell, и атрибутом voids, представленным множеством, состоящим из более чем одного объекта oriented_closed_shell.

ЕВ8 - проверка объекта oriented_closed_shell с атрибутом orientation, имеющим значение FALSE.

ЕВ9 - проверка объекта closed_shell с атрибутом cfs_faces, представленным множеством, состоящим из одного объекта face_surface.

ЕВ30 - проверка объекта loop как объекта vertex_loop.

Е.3.2.2 Спецификация входа в препроцессор

Создается объект elementary_brep_shape_representation, состоящий из единственного объекта manifold_solid_brep. Объект manifold_solid_brep должен иметь форму сплошного цилиндра с полусферическим основанием и плоской наклонной верхней гранью. Одно такое граничное представление должно содержать пустоту такой же формы и ориентации. Второй пример должен содержать две непересекающиеся пустоты: одну - такой же формы, вторую - сферической формы. Пустота сферической формы должна быть определена одним объектом face_surface с использованием объекта vertex_loop. Центр полусферы для внешней оболочки находится в начале координат, а ось Z является осью цилиндра. Каждая оболочка определена как единая замкнутая оболочка с тремя гранями. Соответствующее множество размеров определено в приведенной ниже спецификации на языке EXPRESS-I.

Е.3.2.3 Спецификация входа в постпроцессор

Примечания

1 Контекст объекта cylinder_sphere_shell с соответствующими параметрами используется для определения граней внешней оболочки В-rep модели и для определения оболочек пустот.

2 Внешняя оболочка объекта brep_with_voids является объектом closed_shell, но не объектом oriented_closed_shell. Объект oriented_closed_shell используется для определения оболочек пустот, при этом атрибут orientation должно иметь значение FALSE.

E.3.2.4 Критерии решения постпроцессора

EB6 - оболочка пустоты не должна пересекаться с внешней оболочкой; оболочка пустоты должна полностью находиться внутри внешней оболочки.

ЕВ7 - оболочки пустот не должны пересекаться с внешней оболочкой или друг с другом; каждая оболочка пустоты должна полностью находиться внутри внешней оболочки, два объекта elementary_brep_shape_representation ebsr1 и ebsr2 не должны быть пространственно связаны.

ЕВ8 - перпендикуляры к оболочкам пустот должны быть направлены внутрь пустот.

ЕВ9 - объект closed_shell с единственной гранью, геометрия которой определена объектом spherical_surface, должен быть правильно обработан.

ЕВ30 - объект vertex_loop должен быть корректно обработан как объект face_bound, чтобы определить грань как полностью сферическую поверхность.

Е.3.3 Контрольный пример eb3

Контрольный пример eb3 является простым контрольным примером, определяющим грани, необходимые для определения одиночного сплошного сегмента тора, ограниченного плоскостями. Одно из пересечений плоскости с тором представлено плоской полилинией. Определение оболочки обеспечивается контекстом объекта toroidal_segment с использованием исходных параметров.

Е.3.3.1 Цели тестирования

Ниже перечислены цели тестирования, охватываемые данным контрольным примером.

ЕВ28 - проверка объекта elementary_surface как объекта toroidal_surface.

ЕВ33 - проверка объекта edge как объекта oriented_edge с атрибутом orientation, имеющим значение FALSE.

ЕВ34 - проверка объекта edge_curve с атрибутом edge_geometry, представленным как объект line.

ЕВ35 - проверка объекта edge_curve с атрибутом edge_geometry, представленным как объект polyline.

Е.3.3.2 Спецификация входа в препроцессор

Создается объект elementary_brep_shape_representation, состоящий из единственного объекта manifold_solid_brep. Объект manifold_solid_brep должен иметь форму тороидального сегмента с центром, расположенным в начале координат, и центральной осью, направленной по оси Z. Сегмент создан сечением тора тремя плоскостями, одна из которых (z=0) проходит через центр и перпендикулярна к центральной оси. Две другие плоскости параллельны друг другу, причем одна из них (х=0) проходит через центр. Линии пересечений являются дугами окружностей или полилинией. В-rep модель определена одной замкнутой оболочкой с четырьмя гранями. Соответствующее множество размеров определено в приведенной ниже спецификации на языке EXPRESS-I.

Е.3.3.3 Спецификация входа в постпроцессор

Примечание - Для определения граней и всей геометрии и топологии В-rep модели используется контекст объекта toroidal_segment с параметрами, заданными по умолчанию.

E.3.3.4 Критерии решения постпроцессора

EB28 - грань объекта toroidal_surface должна быть обработана и ограничена правильно.

ЕВ33 - если объект edge с атрибутом orientation, имеющим значение FALSE, используется повторно, он должен быть интерпретирован правильно.

ЕВ34 - объект line должен быть правильно обрезан объектами vertice.

ЕВ35 - все точки объекта polyline должны принадлежать объекту toroidal_surface с допустимым отклонением менее чем 0,0000001. Точки полилинии должны быть копланарны.

Е.3.4 Контрольный пример eb4

В контрольном примере eb4 определены грани, необходимые для определения одиночного сплошного тела, полученного путем объединения двух цилиндров разных радиусов с ортогональными осями. Линия пересечения является замкнутой трехмерной кривой, представленной полилинией. Определение оболочки обеспечивается контекстом объекта cylinder_union_polyline с использованием исходных параметров.

Е.3.4.1 Цели тестирования

Ниже перечислены цели тестирования, охватываемые данным контрольным примером:

ЕВ21 - проверка объекта elementary_surface с атрибутом position, представленным как объект axis2_placement_3d с отсутствием атрибута axis.

ЕВ23 - проверка объекта elementary_surface с атрибутом position, представленным как объект axis2_placement_3d с отсутствием атрибута ref_direction.

ЕВ35 - проверка объекта edge_curve с атрибутом edge_geometry, представленным как объект polyline (замкнутая трехмерная полилиния).

Е.3.4.2 Спецификация входа в препроцессор

Создается объект elementary_brep_shape_representation, состоящий из единственного объекта manifold_solid_brep. Объект manifold_solid_brep должен иметь форму двух перпендикулярных пересекающихся цилиндров. Для определения положения одного из этих цилиндров при определении объекта axis2_placement_3d должны быть использованы параметры, заданные по умолчанию. Линия пересечения должна быть представлена полилинией. Соответствующее множество размеров определено в приведенной ниже спецификации на языке EXPRESS-I.

Е.3.4.3 Спецификация входа в постпроцессор

Примечание - Для определения граней и всей геометрии и топологии В-rep модели используется контекст объекта cylinder_union_polyline с параметрами, заданными по умолчанию.

Е.3.4.4 Критерии решения постпроцессора

ЕВ21 - значения по умолчанию атрибута axis должны быть заданы правильно.

ЕВ23 - значения по умолчанию атрибута ref_direction должны быть заданы правильно.

ЕВ35 - все точки полилинии должны принадлежать обоим объектам cylindrical_surface с допустимым отклонением менее чем 0,000001.

Е.3.5 Контрольный пример еb5

В контрольном примере eb5 определены грани, необходимые для определения сплошных тел, полученных в результате пересечения наклонных плоскостей с конусом. Кривые, ограничивающие грани, могут быть эллипсами, гиперболами, параболами, дугами окружностей и сегментами прямых линий. Определение оболочек обеспечивается контекстом объекта cone_faces с использованием исходных параметров.

Е.3.5.1 Цели тестирования

Ниже перечислены цели тестирования, охватываемые данным контрольным примером.

ЕВ2 - проверка объекта elementary_brep_shape_representation с атрибутом context, представленным как объект geometric_context с атрибутом items, представленным множеством, состоящим более чем из одного объекта manifold_solid_brep.

ЕВ15 - проверка объекта face как объекта face_surface с атрибутом bounds, представленным множеством, состоящим, по меньшей мере, из двух объектов face_bound, включая один объект vertex_loop.

ЕВ26 - проверка объекта elementary_surfaсе как объекта conical_surface.

ЕВ40 - проверка объекта conic как объекта ellipse.

ЕВ41 - проверка объекта conic как объекта hyperbola.

ЕВ42 - проверка объекта conic как объекта parabola.

Е.3.5.2 Спецификация входа в препроцессор

Создается объект elementary_brep_shape_representation, состоящий из двух объектов manifold_solid_brep. Объекты manifold_solid_brep должны иметь форму конусов, ограниченных наклонными плоскостями. Плоскости выбираются так, чтобы линии пересечения имели форму эллипса, параболы, гиперболы и дуг окружности. Первый конус имеет вершину, образованную объектом vertex_loop, и эллиптическое основание. У второго конуса вершина образована эллиптической кривой, как и его основание. Соответствующее множество размеров определено в приведенной ниже спецификации на языке EXPRESS-I.

Е.3.5.3 Спецификация входа в постпроцессор

Примечание - Для определения граней и всей геометрии и топологии В-rep модели используется контекст объекта cone_shell с параметрами, заданными по умолчанию.

E.3.5.4 Критерии решения постпроцессора

EB2 - две В-rep модели должны точно соприкасаться поверхностью общей грани, две В-rep модели не должны пересекаться.

ЕВ15 - объект face с атрибутом face_bound, представленным как объект vertex_loop, должен быть правильно обработан.

ЕВ26 - объекты conical_surface должны быть правильно обрезаны ограничивающими ребрами.

ЕВ40 - все точки на эллипсе должны быть расположены точно на обоих объектах conical_surface и на объекте plane, пересекающем их.

ЕВ41 - все точки гиперболических ребер должны одновременно принадлежать объектам conical_surface и пересекающему объекту plane, а объект hyperbola должен быть правильно обрезан посредством объектов vertex_point.

ЕВ42 - все точки параболических ребер должны одновременно принадлежать объектам conical_surface и пересекающему объекту plane, а объект parabola должен быть правильно обрезан посредством объектов vertex_point.

Е.3.6 Контрольный пример eb6

Контрольный пример eb6 разработан для проверки использования объектов mapped_item при создании простой сборки из элементарных В-rep моделей. Он также обеспечивает проверку непротиворечивости объектов geometric_representation_context для разных координатных пространств. Данный тест использует контекст объекта cylinder_union_polyline для определения геометрии и топологии.

Е.3.6.1 Область охвата целей тестирования

Ниже перечислены цели тестирования, охватываемые данным контрольным примером:

ЕВ3 - проверка объекта elementary_brep_shape_representation с атрибутом context, представленным как объект geometric_representation_context с атрибутом items, представленным как объект mapped_item.

ЕВ4 - проверка объекта elementary_brep_shape_representation с атрибутом context, представленным как объект geometric_representation_context с двумя или более элементами, представленными как объекты manifold_solid_brep, или mapped_item, или axis2_placement_3d. При этом по меньшей мере один из них должен быть объектом axis2_placement_3d.

Е.3.6.2 Спецификация входа в препроцессор

Создается основной объект elementary_brep_shape_representation, состоящий из объекта manifold_solid_brep в форме двух пересекающихся цилиндров, определенных в контрольном примере еb4. Затем определяется объект mapped_item как поступательно перемещенная и повернутая копия данного представления. После этого определяются два следующих объекта elementary_brep_shape_representation; один, определенный в том же контексте, состоит только из объекта mapped_item, а другой, определенный в другом контексте, содержит исходные объекты manifold_solid_brep, mapped_item и axis2_placement_3d. Полные сведения о размерах и отображении определены в приведенной ниже спецификации на языке EXPRESS-I.

Е.3.6.3 Спецификация входа в постпроцессор

Примечания

1 В приведенной ниже спецификации два разных объекта geometric_representation_context созданы для геометрических определений.

2 Для определения граней и всей геометрии и топологии В-rep модели используется контекст объекта cylinder_union_polyline с параметрами, заданными по умолчанию.

3 Объект ebsr1 должен быть повернутой и поступательно перемещенной копией объекта ebsr.

4 Объект ebsrass должен быть эквивалентен двум копиям объекта ebsr, "склеенным" вместе.

E.3.6.4 Критерии решения постпроцессора

ЕВ3 - после обработки объект mapped_item должен быть правильно интерпретирован, результатом является повернутая и поступательно перемещенная копия исходной В-rep модели.

ЕВ4 - объект elementary_brep_shape_representation, содержащий объект mapped_item, В-rep модель и объект axis2_placement_3d должны быть правильно интерпретированы, результатом является исходная В-rер модель и повернутая и поступательно перемещенная копия исходной В-rep модели, которая касается грани.

ЕВ3 и ЕВ4 - два разных объекта elementary_brep_shape_representation не должны быть пространственно связаны.

Е.3.7 Контрольный пример eb7

Контрольный пример eb7 разработан для проверки использования объектов mapped_item совместно с объектом cartesian_transformation_operator при создании простой сборки из многогранных В-rep моделей. Проверяется использование коэффициента масштабирования. В данном тесте используется контекст объекта cylinder_sphere_shell для определения геометрии и топологии.

Е.3.7.1 Цели тестирования

Ниже перечислены цели тестирования, охватываемые данным контрольным примером:

ЕВ44 - проверка объекта mapped_item с атрибутом mapping_target, представленным как объект cartesian_transformation_operator_3d.

EB45 - проверка объекта cartesian_transformation_operator как объекта cartesian_transformation_operator_3d с масштабом, представленным значением типа REAL, не равным 1,0.

Е.3.7.2 Спецификация входа в препроцессор

Создается объект elementary_brep_shape_representation, состоящий из единственного объекта manifold_solid_brep. B-rep модель должна иметь форму сплошного цилиндра с полусферическим основанием и плоским наклонным верхом. Центр полусферы находится в начале координат, а ось цилиндра должна располагаться вдоль оси Z. Затем данное представление используется совместно с объектами mapped_item и cartesian_transformation_operator для создания в том же контексте объекта representation_context представления, состоящего из повернутой, поступательно перемещенной и масштабированной (но не с коэффициентом 1,0) копии исходного представления и исходной В-rep модели. Поступательное перемещение и значение коэффициента масштабирования выбираются так, чтобы цилиндры из двух В-rep моделей соприкасались, но не пересекались.

Е.3.7.3 Спецификация входа в постпроцессор

Примечание - Для определения граней и всей геометрии и топологии В-rep модели используется контекст объекта cylinder_sphere_shell с параметрами, заданными по умолчанию. Объект csrans должен быть повернутой, масштабированной и поступательно перемещенной копией объекта cysp_solid.

E.3.7.4 Критерии решения постпроцессора

EB44 - после обработки, сплошная В-rep модель, определенная посредством объекта mapped_item, должна быть корректно масштабирована и размещена.

ЕВ45 - после обработки объект absrass должен состоять из двух сплошных В-rep моделей цилиндрической формы с полусферическим основанием, которые касаются друг друга в плоскости х=25. Одна из них является копией масштаба 4/5 другой модели, полученной после поступательного перемещения и поворота.

Е.4 Контексты, определенные для контрольных примеров элементарных В-rep моделей

Приведенные ниже контексты на языке EXPRESS-I использованы в контрольных примерах раздела Е.3.

E.4.1 Контекст объекта cylinder_sphere_shell

Данный контекст описывает грани, необходимые для определения простого объекта closed_shell цилиндрической формы с полусферическим основанием, имеющим центр, расположенный в точке (orc,orc,orc), радиус rad и осевую высоту к наклонной грани h.

Все границы определены посредством объектов edge_loop и conic.

E.4.2 Контекст объекта cone_shell

Данный контекст описывает грани, необходимые для определения замкнутых оболочек конической формы с круглыми, эллиптическими, гиперболическими или параболическими гранями. Конус имеет вершину с координатами (orc,orc,orc), половинный угол при вершине 30° и ось, параллельную оси z. Перпендикуляр к каждой плоской грани ортогонален к направлению оси у и расположен под фиксированным углом.

Примечание - Объекты plane_angle_unit должны быть определены в градусах.

Размеры результирующей оболочки должны регулироваться изменением значений расстояний dc, de, dh, dp от вершины конуса до точек пересечения с осью конуса плоскостей окружности, гиперболы, параболы соответственно.

Две смежные оболочки могут быть определены простой конической оболочкой с эллиптическим основанием и более сложной конической формой с плоскими гранями эллиптической вершины, круглого основания и гиперболической и параболической сторонами. У основания есть два прямых ребра, параллельных оси у.

Все границы определены посредством объектов edge_loop с использованием объектов line или conic или посредством объекта vertex_loop.

E.4.3 Контекст объекта toroidal_segment

Данный контекст описывает грани, необходимые для определения сегмента тора, ограниченного плоскостями. Объектами edge_curve являются объекты line, circular arcpolyline.

Центр тора расположен в начале координат, а его центральной осью является ось z; максимальный и минимальный радиусы тора равны 100 и 20. Ограничивающие плоскости заданы координатами z=0, х=0 и х=50. Все точки полилиний расположены на поверхности тора с допустимым отклонением менее чем 10Е(-6).

Все границы определены посредством объектов edge_loop. Основные размеры не должны изменяться.

E.4.4 Контекст объекта cylinder_union_polyline

Данный контекст описывает грани, необходимые для определения граней объединения двух цилиндров разных радиусов.

Данный контекст дает пример неплоского объекта polyline и объекта face с тремя ограничивающими контурами.

Все границы определены посредством объектов edge_loop. Основные размеры не должны изменяться.

Приложение ДА
(справочное)

Сведения о соответствии ссылочных международных стандартов ссылочным национальным стандартам Российской Федерации

Таблица ДА.1

Электронный текст документа

и сверен по:

, 2010