ГОСТ Р ИСО 25178-2-2014
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗДЕЛИЙ (GPS)
Структура поверхности. Ареал
Часть 2
Термины, определения и параметры структуры поверхности
Geometrical Product Specifications (GPS). Surface texture. Profile method. Part 2: Terms, definitions and surface texture parameter
ОКС 17.040.20
Дата введения 2016-01-01
Предисловие
1 ПОДГОТОВЛЕН Обществом с ограниченной ответственностью "ЦИТОпроект" (ООО "ЦИТО-проект") на основе собственного аутентичного перевода на русский язык международного стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 453 "Имплантаты в хирургии"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 12 декабря 2014 г. N 2059-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 25178-2:2012* "Геометрические характеристики изделий (GPS). Структура поверхности. Ареал. Часть 2. Термины, определения и параметры структуры поверхности" (ISO 25178-2 "Geometrical Product Specifications (GPS) - Surface texture: Profile method - Part 2: Terms, definitions and surface texture parameters")
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты Российской Федерации, сведения о которых приведены в дополнительном приложении ДА.
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в ГОСТ Р 1.0-2012 (раздел 8). Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (gost.ru)
1 Область применения
Данная часть ИСО 25178 устанавливает термины, определения и параметры для оценки структуры поверхности профильными методами.
2 Нормативные ссылки
Следующие документы*, на которые даны ссылки, являются обязательными для применения этого документа. Датированные ссылки указывают только на цитируемое издание. Недатированные ссылки указывают на последнее издание упоминаемого документа (включая любые поправки).
_______________
* Таблицу соответствия национальных стандартов международным см. по ссылке. - .
ИСО/TS 16610-1:2006 Геометрические характеристики изделий (GPS). Фильтрация. Часть 1: Обзор и основные понятия (ISO/TS 16610-1:2006, Geometrical product specifications (GPS) - Filtration - Part 1: Overview and basic concepts)
ИСО 17450-1:2011 Геометрические характеристики изделий (GPS). Общие концепции. Часть 1: Модель геометрической характеристики и ее подтверждения (ISO 17450-1:2011, Geometrical product specifications (GPS) - General concepts - Part 1: Model for geometrical specification and verification)
ИСО 25178-3:- Геометрические характеристики изделий (GPS). Структура поверхности. Ареал. Часть 3. Операторы характеристик (ISO 25178-3:-1), Geometrical product specifications (GPS) - Surface texture: Areal - Part 3: Specification operators)
________________
Будет опубликован.
3 Термины и определения
В настоящем стандарте применены термины по ИСО 17450-1 и ISO/TS 16610-1, а также следующие термины с соответствующими определениями.
3.1 Общие термины
3.1.1 модель неидеальной поверхности, модель кожи (non-ideal surface model skin model): Модель физического контакта изделия с окружающей средой.
[ИСО 17450-1:2011, 3.2.2]
3.1.1.1 механическая поверхность (mechanical surface): Границы эрозии, сферический шар с радиусом r, точки центра идеальной тактильной сферы, также с радиусом r, с перекатом через модель кожи изделия.
[ИСО 14406:2010, 3.1.1]
3.1.1.2 электромагнитная поверхность (electromagnetic surface): Поверхность, полученная путем электромагнитного взаимодействия с моделью кожи изделия.
[ИСО 14406:2010, 3.1.2]
3.1.2 система координат характеристики (specification coordinate system): Система координат, в которой указаны параметры структуры поверхности.
Примечание - Если номинальная поверхность является плоскостью (или частью плоскости), то обычно (на практике) используется прямоугольная система координат, в которой оси образуют правостороннюю декартову систему, ось X и Y также располагаются на номинальной поверхности, а ось Z направлена наружу (от материала к окружающей среде). Данное условие принято в оставшемся фрагменте данной части ИСО 25178.
3.1.3 первичная поверхность (primary surface): Часть поверхности, полученная в том случае, когда данная часть представлена в виде определенной первичной математической модели с определенным индексом размещения.
[ИСО/TS 16610-1:2006, 3.3]
Примечание - в данной части ИСО 25178 для получения первичной поверхности используется S-фильтр.
3.1.3.1 первичная извлеченная поверхность (primary extracted surface): Конечный набор точечных данных, полученных с первичной поверхности.
[ИСО 14406:2010, 3.7]
3.1.4 фильтр поверхности (surface filter): Оператор фильтрации, применяемый к поверхности.
Примечание - на практике оператор фильтра будет применяться к первичной извлеченной поверхности.
3.1.4.1 S-фильтр (S-filter): Поверхностный фильтр, который удаляет с поверхности мелкие латеральные компоненты, приводя к получению первичной поверхности.
3.1.4.2 L-фильтр (L-filter): Поверхностный фильтр, который удаляет с первичной поверхности или S-F-поверхности крупные латеральные компоненты.
3.1.4.3 F-операция (F-operation): Операция, которая удаляет формы с первичной поверхности.
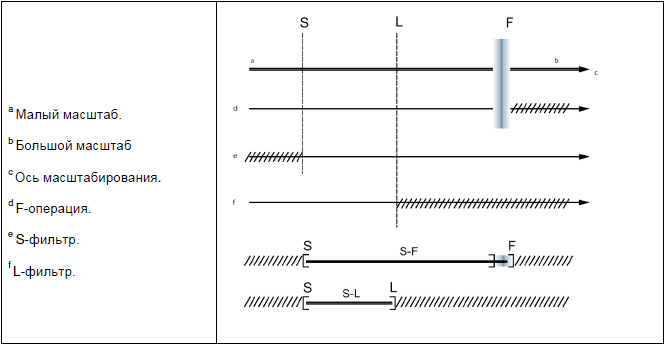
Примечание 1 - Некоторые F-операции (например, операции объединения) имеют действие, весьма отличное от фильтрации. И хотя их действие может ограничивать более крупные масштабы латерального компонента поверхности, данное действие является очень нечетким. Нечеткая линия действия F-операции представлена на рисунке 1.
Примечание 2 - Многие L-фильтры чувствительны к форме и перед применением требуют выполнения F-операции в качестве предварительного фильтрования.
3.1.5 S-F поверхность (S-F surface): Поверхность, полученная из первичной поверхности путем удаления формы при помощи F-операции.
Примечание - Рисунок 1 иллюстрирует связь между S-F поверхностью и S-фильтром, а также F-операцией.
3.1.6 S-L поверхность (S-L surface): Поверхность, полученная из S-F-поверхности путем удаления компонентов большого масштаба при помощи L-фильтра.
Примечание - Поверхность, полученная из S-F-поверхности путем удаления компонентов большого масштаба при помощи L-фильтра. Рисунок 1 иллюстрирует связь между S-L поверхностью и S-фильтром, а также L-фильтром.
Рисунок 1 - связи между S-фильтром, L-фильтром, F-операцией, а также S-F и S-L поверхностями
3.1.7 поверхность ограниченного масштаба (scale-limited surface): S-F поверхность или S-L поверхность
3.1.8 эталонная поверхность (reference surface): Поверхность, связанная с поверхностью ограниченного масштаба в соответствии с критерием.
Примечание 1 - Результат используется в качестве эталонной поверхности для параметров структуры поверхности.
Примечание 2 - Примеры эталонных поверхностей, включая плоскость, цилиндр и сферу.
3.1.9 область оценки (evaluation area): Часть поверхности ограниченного масштаба для определения оцениваемой области.
Примечание - для получения дополнительной информации см. ИСО 25178-3.
3.1.10 область определения (definition area): Часть области оценки для определения параметров, характеризующих поверхность ограниченного масштаба.
3.2 Термины геометрических параметров
3.2.1 параметр поля (field parameter): Параметр, определенный на основании всех точек поверхности ограниченного масштаба.
Примечание - Параметры поля определены в пункте 4.
3.2.2 параметр функции (feature parameter): Параметр, определенный в подгруппе заранее заданных топографических функций на основании поверхности с ограниченным масштабом.
Примечание - Параметры функции определены в пункте 5.
3.2.3 V-параметр (V-parameter): Поле объема материала или объема пустот, или параметр функции.
3.2.4 S-параметр (S-parameter): Параметр поля или функции, который не является V-параметром.
3.2.5 высота (height): Подписанное нормальное расстояние от эталонной поверхности до поверхности с ограниченным масштабом.
Примечание 1 - Расстояние определяется по нормали к эталонной поверхности.
Примечание 2 - Высота отрицательна, если от эталонной поверхности точка располагается в направлении материала.
3.2.6 значение на оси ординат z(x,y) (ordinate value z(x,y): Высота поверхности с ограниченным масштабом в положении х,у.
Примечание - система координат основана на эталонной поверхности.
3.2.7 вектор локального градиента 
(local gradient vector 
):
Градиент поверхности с ограниченным масштабом в положении х,у.
Примечание - Для конкретного применения см. ИСО 25178-3.
3.2.8 функция автокорреляции (
,
) (autocorrelation function
(
,
):
Функция, которая описывает корреляцию между поверхностью и аналогичной поверхностью, преобразованной при помощи (,
)
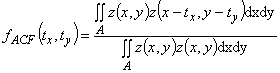
Причем А - область определения.
3.2.9 преобразование Фурье (fourier transformation F(p,q): Оператор, который преобразует поверхность с ограниченным масштабом в пространство Фурье.
причем А - область определения.
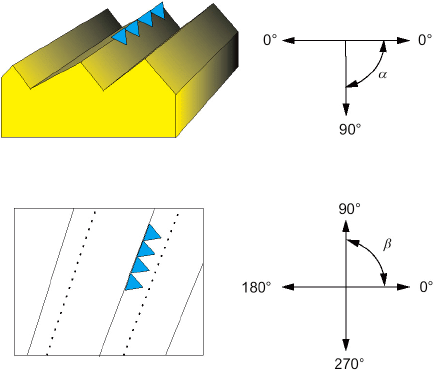
3.2.9.1 угловой спектр 
(angular spectrum fAPS(s): Спектр мощности для заданного направления относительно указанного направления в плоскости области определения.
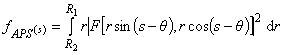
где 
диапазон интеграции в радиальном направлении, a s - указанное направление.
Примечание 1 - Положительная ось х определяется как нулевой угол.
Примечание 2 - Угол является положительным в направлении против часовой стрелки от оси х.
3.3 Термины геометрических признаков
3.3.1 пик (peak): Точка на поверхности, которая выше всех остальных точек поблизости от данной точки.
Примечание 1 - Для дискретных данных необходима триангуляция поверхности.
Примечание 2 - Существует теоретическая возможность плато. На практике этого можно избежать путем использования стремящегося к нулю наклона.
Примечание 3 - Для конкретного применения см. ИСО 25178-3.
3.3.1.1 горб (hill): Область вокруг пика, в которой все варианты траектории максимального подъема заканчиваются на пике.
3.3.1.2 линия курса (course line): Кривая, разделяющая соседние горбы.
3.3.2 провал (pit): Точка на поверхности, которая располагается ниже всех остальных точек поблизости от данной точки.
Примечание 1 - Для дискретных данных необходима триангуляция поверхности.
Примечание 2 - Существует теоретическая возможность плато. На практике этого можно избежать путем использования стремящегося к нулю наклона.
Примечание 3 - Для конкретного применения см. ИСО 25178-3.
3.3.2.1 желоб (dale): Область вокруг провала, в которой все варианты траектории максимального спуска заканчиваются в провале.
Примечание - Мотив ареала - желоб, см. ИСО 12085.
3.3.2.2 линия хребта (ridge line): Кривая, разделяющая соседние желоба.
3.3.3 седло (saddle): Набор точек на поверхности ограниченного масштаба, в которых линии хребта и линии курса пересекаются.
3.3.3.1 точка седла (saddle point): Седло, состоящее из одной точки.
3.3.4 топографическая характеристика (topographic feature): Характеристика ареала, линии или точки на поверхности ограниченного масштаба.
3.3.4.1 характеристика ареала (areal feature): Горб или желоб.
3.3.4.2 характеристика линии (line feature): Линия курса или линия хребта.
3.3.4.3 характеристика точки (point feature): Точка пика, провала или седла.
3.3.5 линия контура (contour line): Линия на поверхности, состоящая из точек равной высоты.
3.3.6 сегментация (segmentation): Метод, который разделяет поверхность ограниченного масштаба на отдельные зоны.
3.3.6.1 функция сегментации (segmentation function): Функция, которая разделяет набор "явлений" на два различных набора, названных значимыми и незначимыми явлениями, и удовлетворяет трем особенностям сегментации.
Примечание 1 - Примеры явлений: значения ординаты, характеристики точки и т.д.
Примечание 2 - Полное математическое описание функции сегментации и трех особенностей сегментации представлено в документе Scott (2004) (см. ссылку [16]).
Примечание 3 - Математическую обработку функции сегментации и особенности сегментации перенесут в будущий документ серии ИСО 16610 по сегментации.
3.3.6.2 первое свойство сегментации Р1 (first segmentation property Р1): Свойство, состоящее в том, что каждое явление относят к набору значимых явлений или набору незначимых явлений, но не к обоим наборам.
,
где Е - набор всех явлений;
- картирование явлений в наборе значимых явлений;
Ф(.) - картирование явлений в наборе незначимых явлений.
3.3.6.3 второе свойство сегментации Р2 (second segmentation property Р2): Свойство, состоящее в том, что если значимое явление удалить из набора явлений, то остальные значимые явления сохраняются в новом наборе значимых явлений.
, 
,
где Е - набор всех явлений;
Ф(.) - картирование явлений в наборе незначимых явлений.
3.3.6.4 третье свойство сегментации Р3 (third segmentation property Р3): Свойство, состоящее в том, что если удалить незначимое явление из набора явлений, то это приводит к получению аналогичного набора значимых явлений.
, 
,
где Е - набор всех явлений;
- картирование явлений в наборе значимых явлений.
3.3.7 дерево изменений (change tree): График, в котором каждая линия контура представлена в качестве точки относительно высоты таким образом, чтобы соседние линии контура представляли собой соседние точки на графике.
Примечание - пики и провалы представлены на дереве изменений к концу линий. Точки седла представлены на дереве изменений при помощи объединяющихся линий. Дополнительные сведения о дереве изменения представлены в приложении А.
3.3.7.1 отсечение (pruning): Метод упрощения дерева изменений, в котором удалены линии от пиков (или провалов) до ближайших соединенных точек седла.
3.3.7.2 локальная высота пика (local peak height): Разница между высотой пика и высотой ближайшего соединенного седла на дереве изменений.
3.3.7.3 локальная высота провала (local pit height): Разница между высотой ближайшего соединенного седла на дереве изменений и высотой провала.
3.3.7.4 отсечение по Вольфу (wolf pruning): Отсечение, при котором линии удаляются в порядке от пика/провала с наименьшей локальной высотой пика/провала до пика/провала с указанной локальной высотой.
Примечание - локальная высота пика/провала будет изменяться в процессе отсечения Вольфа, поскольку удаляемые линии из дерева изменения также приведут к удалению связанной точки седла.
3.3.8 высота пика по Вольфу (wolf peak height): Минимальный порог, при котором пик отсекается при помощи правила отсечения Вольфа.
3.3.9 высота провала по Вольфу (Wolf pit height): Минимальный порог, при котором пик отсекается при помощи правила отсечения Вольфа.
3.3.10 высота пика (peak height): Высота пика.
3.3.11 высота провала (pit height): Высота провала.
3.3.12 различение высот (height discrimination): минимальная высота пика по Вольфу или минимальная высота провала по Вольфу на поверхности ограниченного масштаба, которую следует брать в расчет.
Примечание - различение высот обычно указано в процентах от Sz (4.1.6).
4 Определения параметров поля
В терминологических записях, представленных ниже, за каждым термином следует его параметр (сокращенный термин), а затем его символ. И хотя сокращенные термины могут содержать множество букв, символы включают только одну букву с индексом (при необходимости). Символы используются в уравнениях, представленных в настоящем документе. Причина такого разделения состоит в том, чтобы избежать неправильной интерпретации составных букв как знака умножения между количественными параметрами в уравнениях. Параметры (сокращенные термины) используются в документации изделия, рисунках и листах технических данных.
4.1 Параметры высоты
Все параметры высоты определены в области определения.
4.1.1 Среднеквадратичное значение высоты поверхности ограниченного масштаба Sq, (root mean square height of the scale-limited surface Sq, Sq): Среднеквадратичное значение ординаты в области определения (А)
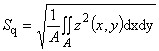
4.1.2 асимметрия поверхности ограниченного масштаба Ssk, (skewness of the scale-limited surface Ssk, Ssk): Отношение среднего ординаты в третьей степени и куба Sq в области определения (А)
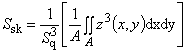
4.1.3 эксцесс поверхности ограниченного масштаба Sku, (kurtosis of the scale-limited surface Sku, Sku): Отношение среднего значения ординаты в четвертой степени и Sq в четвертой степени в области определения (А)
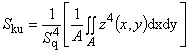
4.1.4 максимальная высота пика поверхности ограниченного масштаба Sp, (maximum peak height of the scale limited surface Sp, Sp): Наибольшее значение высоты пика в области определения.
4.1.5 максимальная высота провала поверхности ограниченного масштаба ,
(maximum pit height of the scale limited surface Sv, Sv): Отрицательное значение наибольшей высоты провала в области определения.
4.1.6 максимальная высота поверхности ограниченного масштаба Sz, (maximum height of the scale-limited surface Sz, Sz): Сумма максимальной высоты пика и максимальной высоты провала в области определения.
4.1.7 арифметическое среднее значение высоты поверхности ограниченного масштаба Sa, (arithmetical mean height of the scale limited surface Sa, Sa): Арифметическое среднее абсолютного значения ординаты в области определения (А)
4.2 Пространственные параметры
Все пространственные параметры определены в области определения.
4.2.1 длина автокорреляции Sal, (autocorrelation length Sal, Sal): Горизонтальное расстояние
, которое быстрее всегда уменьшается до указанного значения s, 0 1
* где 
_______________
* Формула соответствует оригиналу. - .
Примечание 1 - Если не указано иное, значение s по умолчанию представлено в ИСО 25178-3.
Примечание 2 - Графическое отражение процедуры расчета Sal представлено на рисунке 2.
а) Функция автокорреляции поверхности
b) Порог автокорреляции при s (черные точки расположены выше порога)
с) Пороговая граница центральной части порога
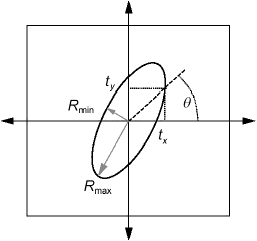
d) Полярные координаты, ведущие к длине автокорреляции в различных направлениях
Рисунок 2 - Процедура расчета Sal и Str
4.2.2 соотношение геометрических размеров структуры Str, (texture aspect ratio Str, Str): Отношение горизонтального расстояния
, которое быстрее всего снижается до указанного значения s, к горизонтальному расстоянию 
с наименьшей скоростью снижения до s, при этом 0 1
,
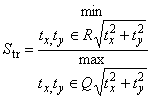где
и .
** - особенность, согласно которой 
на прямой линии, соединяющей точку 
с началом координат.
Примечание 1 - Если не указано иное, значение s по умолчанию представлено в ИСО 25178-3.
Примечание 2 - Графическое отражение процедуры расчета Str представлено на рисунке 2.
4.3 Гибридные параметры
4.3.1 среднеквадратичный градиент поверхности ограниченного масштаба Sdq, (root mean square gradient of the scale-limited surface Sdq, Sdq): Среднеквадратичное значение градиента поверхности в области определения (А) поверхности ограниченного масштаба
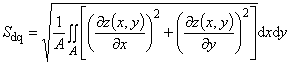
4.3.2 развернутое соотношение пограничной площади поверхности ограниченного масштаба Sdr, (developed interfacial area ratio of the scale-limited surface Sdr, Sdr): Отношение прироста пограничной площади поверхности ограниченного масштаба в области определения (А) к области определения
Примечание - для практического использования данного параметра см. ссылку [10].
4.4 Функции и связанные с ними параметры
4.4.1 функция коэффициента смятия ареала на поверхности ограниченного масштаба (areal material ratio function of the scale-limited surface): Функция, которая отражает коэффициент смятия ареала поверхности ограниченного масштаба как функцию высоты.
Примечание - Данную функцию можно интерпретировать как функцию интегральной вероятности ординат z(x,y) образца в области определения.
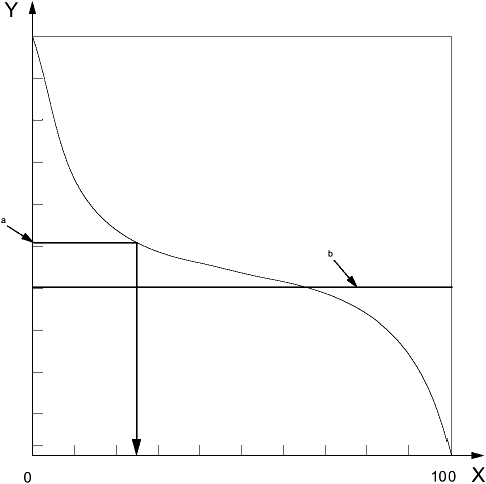
4.4.2 коэффициент смятия ареала поверхности ограниченного масштаба Smr(c), 
(areal material ratio of the scale-limited surface Smr(c), Smr(c)): Отношение площади материала при указанной высоте с к области оценки.
Примечание 1 - Smr(c) обычно выражается в процентах.
Примечание 2 - Высоту берут из эталонной плоскости. См. рисунок 3.
Примечание 3 - Данная функция связана с интегральной функцией вероятности ординат образца.
Условные обозначения: X - коэффициент смятия ареала Smr(c), в процентах; Y - высота; Указанная высота, с;
Эталонная плоскость.
Рисунок 3 - Коэффициент смятия ареала
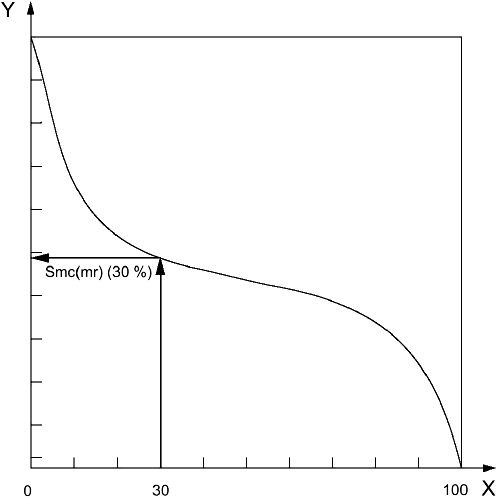
4.4.3 обратный коэффициент смятия ареала поверхности ограниченного масштаба Smc(mr), 
(inverse areal material ratio of the scale-limited surface Smc(mr), Smc(mr)): Высота c, при которой достигается заданный коэффициент смятия ареала (material ratio, mr).
Примечание - Высоту берут с эталонной плоскости (см. рисунок 4).
Условные обозначения: X - коэффициент смятия ареала Smc(mr), в процентах; Y - высота.
Рисунок 4 - Обратный коэффициент смятия ареала
4.4.4 параметр ареала для стратифицированной функциональной поверхности ограниченного масштаба (areal parameter for scale-limited stratified functional surfaces): Параметр, который отражает коэффициент смятия ареала стратифицированной функциональной поверхности ограниченного масштаба как функцию высоты.
4.4.4.1 поверхность ядра (core surface): Поверхность ограниченного масштаба, за исключением выступающих за пределы ядра горбов и желобов (см. рисунок 5).
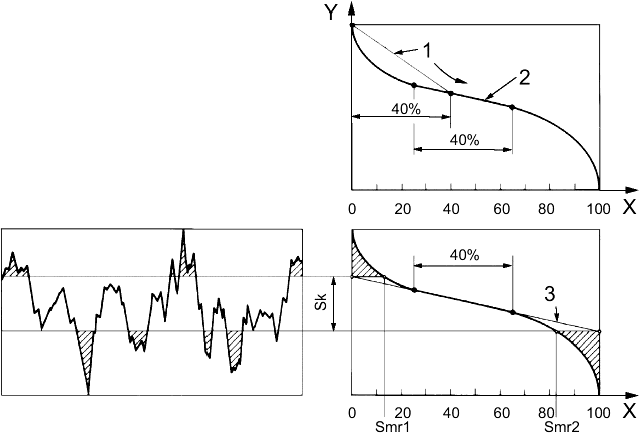
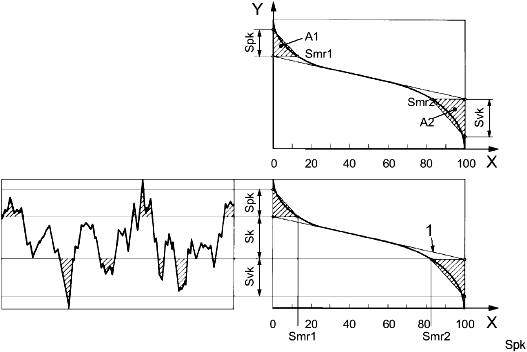
4.4.4.2 высота ядра Sk, (core height Sk, Sk): Расстояние между наибольшим и наименьшим уровнем поверхности ядра (см. рисунок 5).
Условные обозначения: X - коэффициент смятия ареала; Y - положение линии пересечения. 1 - секанс; 2 - секанс с наименьшим градиентом; 3 - эквивалентная прямая линия; Sk - высота ядра; Smr1, Smr2 - коэффициенты смятия. Для простоты иллюстрации данный рисунок демонстрирует профиль, а не площадь поверхности. Принцип аналогичен для площади поверхности.
Рисунок 5 - Расчет значений Sk, Smr1 и Smr2
4.4.4.3 сниженная высота пика Spk, (reduced peak height Spk, Spk): Среднее значение высоты выступающих пиков над поверхностью ядра.
Примечание - Процесс усреднения в пункте 5 снижает влияние выбросов на данный параметр.
4.4.4.4 сниженная высота желоба Svk, (reduced dale height Svk, Svk): Среднее значение высоты выступающих желобов ниже поверхности ядра.
Примечание - Процесс усреднения в пункте 5 снижает влияние выбросов на данный параметр.
4.4.4.5 коэффициент смятия Smr1, (material ratio Smr1, Smr1): Отношение <пиков> области материала на линии пересечения, которая отделяет выступающие горбы от поверхности ядра, к области оценки.
Примечание - Отношение выражено в процентах.
4.4.4.6 Коэффициет смятия Smr2, (material ratio Smr2, Smr2): Отношение <желобов> области материала на линии пересечения, которая отделяет выступающие желоба от поверхности ядра, к области оценки.
Примечание - Отношение выражено в процентах.
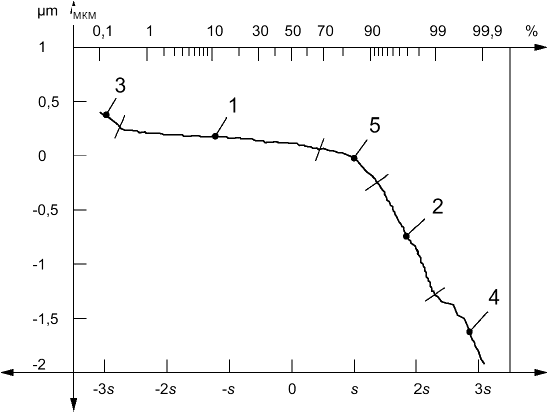
4.4.4.7 кривая вероятности смятия ареала (areal material probability curve): Отображение кривой коэффициента смятия ареала, в которой коэффициент области смятия выражается в виде гауссовой вероятности в значениях стандартного отклонения, отложенных линейно на горизонтальной оси.
Примечание - Данная шкала выражается линейно в стандартных отклонениях согласно распределению Гаусса. В данной шкале кривая коэффициента смятия ареала при гауссовом распределении становится прямой линией. Для стратифицированных поверхностей, представленных двумя распределениями Гаусса, кривая вероятности коэффициента смятия ареала покажет две линейных области (см. 1 и 2 на рисунке 6).
Условные обозначения: 1 - область плато; 2 - область желоба; 3 - остатки или выходящие за определенные пределы пики в данных (поверхность ограниченного масштаба); 4 - глубокие насечки или выходящие за определенные пределы желоба в данных (поверхность ограниченного масштаба); 5 - нестабильная область (изгиб), включенная в точку перехода плато-желоб на основании комбинации двух распределений.
Рисунок 6 - Кривая вероятности коэффициента смятия ареала
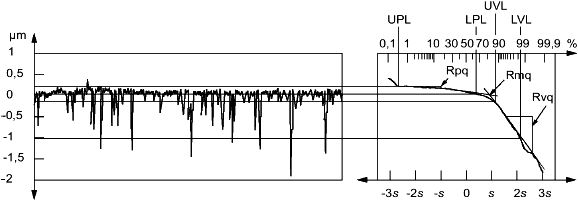
4.4.4.8 среднеквадратичное отклонение желоба Svq, (dale root mean square deviation Svq, Svq): Угол наклона линии регрессии в области желоба (см. рисунок 7).
Примечание - Таким образом, значение Svq можно интерпретировать как значение Sq, в микрометрах, случайного процесса, который образует компонент желоба на поверхности.
4.4.4.9 среднеквадратичное отклонение плато Spq, (plateau root mean square deviation Spq, Spq): Угол наклона линии регрессии в области плато.
См. рисунок 7.
Примечание - Таким образом, значение Spq можно интерпретировать как значение Sp (в микрометрах) случайного процесса, который образует компонент плато на поверхности.
4.4.4.10 коэффициент смятия Smq, (material ratio Smq, Smq): Коэффициент смятия ареала <плато-желоб> на пересечении плато и желоба (см. рисунок 7).
Примечание - Коэффициент выражен в процентах.
4.4.5 объем пустот Vv(p), 
(void volume Vv(p), Vv(p)): Объем пустот на единицу площади при заданном коэффициенте смятия, рассчитанном на основании кривой коэффициента смятия ареала
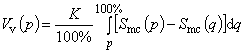
где K - коэффициент пересчета в миллиметры на квадратный метр.
4.4.5.1 объем пустот желоба поверхности ограниченного масштаба Vvv, (dale void volume of the scale-limited surface Vvv, Vvv): Объем желоба при коэффициенте смятия р
.
Примечание - Значения р по умолчанию представлены в ИСО 25178-3.
4.4.5.2 объем пустот ядра поверхности ограниченного масштаба Vvc, (core void volume of the scale-limited surface Vvc, Vvc): Различие объема пустот между коэффициентами смятия р и q
.
Примечание - значения р и q по умолчанию представлены в ИСО 25178-3.
Условные обозначения: LPL - нижний предел плато; LVL - нижний предел желоба; UPL - верхний предел плато; UVL - верхний предел желоба; Rmq - относительный коэффициент смятия в месте пересечения плато и желоба; Rpq - угол наклона линии регрессии в области плато; Rvq - угол наклона линии регрессии в области желоба.
Для простоты иллюстрации данный рисунок демонстрирует профиль, а не площадь поверхности. Принцип аналогичен для площади поверхности.
Рисунок 7 - Поверхность ограниченного масштаба и соответствующая кривая вероятности смятия ареала, а также области, использованные при определении параметров Spq, Svq и Smq
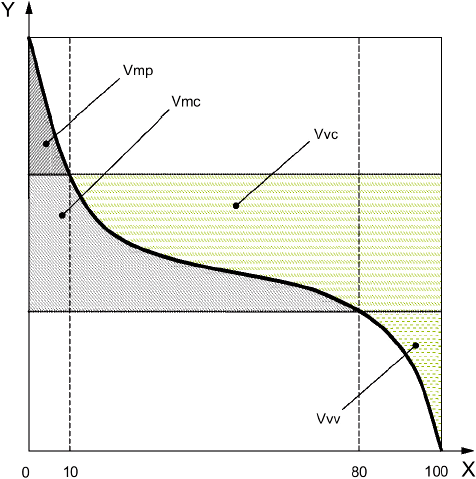
4.4.6 объем материала Vm(p), 
(material volume Vm(p), Vm(p)): Объем материала на единицу площади при заданном коэффициенте смятия, рассчитанном на основании кривой коэффициента смятия ареала
,
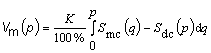где K - коэффициент пересчета в миллиметры на квадратный метр.
Примечание - См. рисунок 8.
Условные обозначения: X - коэффициент смятия ареала, в процентах; Y - высота.
Рисунок 8 - Параметры объема пустот и объема материала
4.4.6.1 объем материала пика поверхности ограниченного масштаба Vmp, (peak material volume of the scale-limited surface Vmp, Vmp): Объем материала при значении р
Примечание - Значение р по умолчанию представлено в ИСО 25178-3.
4.4.6.2 объем материала ядра поверхности ограниченного масштаба Vmc, (core material volume of the scale-limited surface Vmc, Vmc): Различие объема материала между коэффициентами смятия р и q
.
Прмечание - Значениея p и q по умолчанию представлены в ИСО 25178-3.
4.4.7 максимальная высота пика Sxp, (peak extreme height Sxp, Sxp): Различие высоты между коэффициентами смятия р и q
.
Примечание - Значения р и q по умолчанию представлены в ИСО 25178-3.
4.4.8 функция градиента плотности (gradient density function): Градиент плотности рассчитывается для поверхности ограниченного масштаба и показывает относительную частоту относительно угла самого крутого градиента (х, у), а также направление самого крутого градиента
(х, у) против часовой стрелки от оси х (рисунок 9).
Примечание 1 - Пример функции градиента плотности представлен на рисунке 9.
Примечание 2 - Самый крутой градиент , а также направление самого крутого градиента
представлены на рисунке 10.
Условные обозначения: X - направление самого крутого градиента , в градусах; Y - самый крутой градиент
, в градусах; Z - частота возникновения.
Рисунок 9 - Пример функции градиента плотности
Рисунок 10 - Самый крутой градиент , и направление самого крутого градиента
4.4.9 Фрактальные методы
4.4.9.1 функция масштаба-объема Svs(c), 
(volume-scale function Svs(c), Svs(c)): Объем между морфологическим закрытием и открытием поверхности ограниченного масштаба при помощи квадратной горизонтальной плоскости как структурного элемента в зависимости от размера структурного элемента.
Примечание - Функцию зависимости объема от масштаба обычно представляют на графике при помощи двойных логарифмических шкал.
4.4.9.2 функция относительной площади Srel(c), 
(relative area function Srel(c), Srel(c)): Отношение площади, рассчитанной путем разделения поверхности на треугольные плитки в определенном масштабе длины, к области определения как функция масштаба длины.
Примечание - Функцию относительной площади обычно представляют на графике при помощи двойных логарифмических шкал.
4.4.9.3 масштаб длины наблюдения (length scale of observation): Масштаб длины, при котором выполняют расчеты функции масштаба объема или относительной площади.
4.4.9.4 сложность фрактала объема Svfc, (volume fractal complexity Svfc, Svfc): Параметр сложности, полученный при помощи функции масштаба объема, равен умноженному на 1000 углу наклона двойного логарифмического графика зависимости объема от масштаба длины наблюдения.
4.4.9.5 сложность фрактала ареала Safc, (areal fractal complexity Safc, Safc): Параметр сложности, полученный при помощи функции относительной площади, равен умноженному на 1000 углу наклона двойного логарифмического графика зависимости относительного объема от масштаба длины наблюдения.
4.4.9.6 масштаб перехода (crossover scale): Масштаб длины наблюдения, при котором происходит изменение угла наклона функции относительной площади или функции масштаба объема.
Примечание - Поскольку изменение угла наклона не всегда является резким относительно масштаба, необходимо проводить процедуру определения масштаба, при котором происходит изменение.
4.4.9.7 масштаб перехода от гладкой к шероховатой поверхности ,
(smooth-rough crossover scale fSRC, fSRC): Первый масштаб перехода встречается при переходе от сравнительно более крупных масштабов, где поверхность является гладкой, до более мелких масштабов, где поверхность шероховатая.
Примечание - fSRC - это масштаб, выше которого фрактальные размеры примерно равны евклидовым, а также масштаб, ниже которого фрактальные размеры значимо превышают евклидовы. Порог относительной площади используется для определения SRC в масштабе длины, а также анализах относительной площади (см. приложение В).
4.4.9.8 Порог Th, (threshold Th, Th): Значение относительной площади или объема, используемых при определении масштаба перехода от гладкой к шероховатой поверхности.
Примечание 1 - При переходе от наибольших масштабов к наименьшим для оценки SRC используется первое значение относительной площади или объема, превышающее порог.
Примечание 2 - Значение относительной площади или объема может быть установлено для порога либо порог может быть выбран как некоторый процент P от функции наибольшей относительной площади или объема (F) при помощи следующего уравнения
=
.
Примечание 3 - Пороговое значение по умолчанию представлено в ИСО 25178-3.
4.5 Различные параметры
4.5.1 направление структуры поверхности ограниченного масштаба Std, (texture direction of the scale-limited surface Std, Std): Угол, относительно указанного направления
, абсолютного максимального значения углового спектра.
Примечание - Установка 
максимально увеличивает абсолютное значение 
.
5 Определение параметров ареала для стратифицированных функциональных поверхностей ограниченного масштаба
5.1 Расчет параметров Sk, Smr1 и Smr2
Эквивалентная прямая линия, рассчитанная в соответствии с пунктом 5.2, пересекает 0% и 100% линий по оси Smr (см. рисунок 5). От этих точек две линии следуют параллельно оси X; они определяют поверхность ядра путем разделения выступающих горбов и желобов.
Вертикальное расстояние между данными линиями пересечения - высота ядра Sk. Их пересечение с кривой коэффициента смятия определяет коэффициенты смятия Smr1 и Smr2.
5.2 Расчет эквивалентной прямой линии
Эквивалентная прямая линия рассчитывается для центрального региона кривой коэффициента смятия ареала, которая включает 40% измеренных точек поверхности. Данная "центральная область" располагается там, где секанс кривой коэффициента смятия ареала более 40% коэффициента смятия ареала демонстрирует наименьший градиент (см. рисунок 5). Это определяется путем перемещения секущей линии для 
40% вдоль кривой коэффициента смятия ареала, начиная в положении 
0% (см. рисунок 5). Секущая линия для 
40%, имеющая наименьший градиент, определяет "центральную область" кривой коэффициента смятия ареала для расчета эквивалентности. При наличии множества области с эквивалентными минимальными градиентами выбирают область, которая встретилась первой. Затем для данной "центральной области" рассчитывается прямая линия, которая дает наименьшее квадратичное отклонение в направлении ординат поверхности.
Для обеспечения валидности кривой коэффициента смятия ареала выбирают достаточно малый класс ширины ординат поверхности ограниченного масштаба, чтобы по меньшей мере 10 классов попадали в "центральную область". Для поверхностей с почти идеальным геометрическим плато, столь мелкая классификация может быть неприменима в связи с ограниченным разрешением системы измерения. В данном случае в результатах теста следует указывать число классов, используемых при расчете эквивалентной прямой линии.
5.3 Расчет параметров Spk и Svk
На рисунке 5 представлены заштрихованные зоны, расположенные выше и ниже области кривой коэффициента смятия ареала, которая ограничивает высоту ядра . Они соответствуют площади поперечного сечения поверхности горбов и провалов, которые выступают за пределы поверхности ядра.
Каждый из параметров Spk и Svk рассчитывают как высоту прямоугольного треугольника, построенного так, что его площадь равна "площади горба" или "площади провала" соответственно (см. рисунок 11). Прямоугольный треугольник, соответствующий "площади горба А1", имеет в основании Smr1, а соответствующий "площади провала А2" имеет в качестве основания разницу между 100% и значением Smr2.
Параметры Sk, Spk, Svk, Smr1 и Smr2 должны рассчитываться лишь в том случае, если кривая коэффициента смятия ареала имеет S-образную форму, как на рисунках 5 и 11, т.е. имеется только одна точка изгиба. Опыт показал, что такая форма всегда наблюдается в случае перекрытых внахлест, полированных или шлифованных поверхностей.
5.4 Расчет параметров Spq, Svq и Smq
На кривой вероятности смятия ареала, изображенной на рисунке 6 для измеренных данных поверхности двух процессов, могут присутствовать три нелинейных эффекта. Эти эффекты должны устраняться путем ограничения подогнанных частей кривой вероятности смятия ареала при помощи только статистически обоснованной гауссовой части кривой вероятности смятия ареала, за исключением ряда влияний.
На рисунке 6 представлены нелинейные эффекты, причины которых следующие:
- остатки или выходящие за определенные пределы горбы в данных (поверхность ограниченного масштаба) (маркировка 3);
- глубокие насечки или выходящие за определенные пределы желоба в данных (поверхность ограниченного масштаба) (маркировка 4); а также
- нестабильная область (изгиб), включенная в точку перехода плато-желоб на основании комбинации двух распределений (маркировка 5).
Эти исключения позволяют стабилизировать параметры для повторных измерений данной поверхности.
Рисунок 7 демонстрирует профиль и соответствующую кривую вероятности смятия ареала с областями плато и желобов, а также части поверхности, которые определяют две области. Профиль имеет горб, выходящий за установленные пределы. Рисунок демонстрирует отсутствие его влияния на параметры. Рисунок 7 также показывает, что нижнюю часть самых глубоких желобов, которая будет значимо варьировать в зависимости от места выполнения измерений на поверхности, при определении параметров можно игнорировать. Для простоты иллюстрации рисунок 7 демонстрирует профиль, а не площадь поверхности. Принцип аналогичен для площади поверхности.
Процесс определения пределов линейных областей представлен в ИСО 13565-3:1998, приложение А.
Условные обозначения: X - коэффициент смятия; Y - положение линии пересечения; 1 - эквивалентная прямая линия; А1 - площадь горба; А2 - площадь желоба; Smr1, Smr2 - коэффициенты смятия; Sk - относительный коэффициент смятия в месте пересечения плато и желоба; Spk - угол наклона линии регрессии в области плато; Svk - угол наклона линии регрессии в области желоба.
Преобразование "области горба" и "области желоба" в эквивалентный прямоугольный треугольник.
Рисунок 11 - Расчет Spk и Svk на основании данных для Rpk и Rvk
6 Описание характеристик
6.1 Общие требования
Описание характеристик не имеет специфических параметров, однако вместо этого существует арсенал технологий распознавания образа, который можно использовать для изучения особых характеристик на поверхности ограниченного масштаба. Процесс описания характеристик имеет пять стадий:
- выбор типа характеристики структуры;
- сегментация;
- определение значимых характеристик;
- выбор показателей характеристик;
- количественная оценка статистических параметров показателей характеристик.
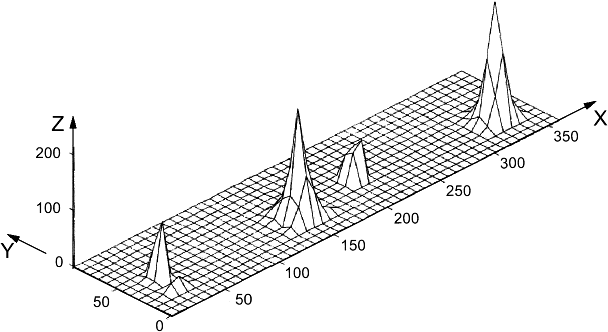
Поверхность, представленная на рисунке 12, используется в качестве иллюстративного примера в данном разделе.
Рисунок 12 - Пример иллюстративной поверхности
6.2 Тип характеристики структуры
Три основных типа характеристик структуры - это характеристики ареала (горбы и желоба), характеристики линии (линии курса и хребта), а также характеристики точки (пики, провалы и точки седла); см. таблицу 1. Для работы с оцениваемой поверхностью важно выбрать соответствующий тип характеристики структуры.
Таблица 1 - Типы характеристик ограниченного масштаба
Класс ограниченной характеристики | Тип характеристики ограниченного масштаба | Обозначение |
Ареал | Горб | Н |
Желоб | D | |
Линия | Линия курса | С |
Линия хребта | R | |
Точка | Пик | Р |
Провал | V | |
Точка седла | S |
6.3 Сегментация
Сегментация используется для определения областей поверхности ограниченного масштаба, которые определяют характеристики ограниченного масштаба. Процесс сегментации начинается с поиска всех горбов и желобов на поверхности ограниченного масштаба. Это обычно приводит к избыточной сегментации поверхности и отсечению "более мелких" сегментов, чтобы оставить соответствующую сегментацию поверхности ограниченного масштаба. Некоторые критерии размеров представлены в таблице 2, которую можно использовать для определения порога и "более мелких" сегментов для отсечения. Например, при помощи поверхности, представленной на рисунке 12, на рисунке 13 изображены горбы, полученные методом отсечения по Вольфу с использованием 10% .
Таблица 2 - Критерии размера сегментации
Критерии размера | Обозначение | Порог |
Отношение высоты локального пика/провала (отсечение Вольфа), см. рисунок 13 | WoIfprune | % Sz |
Объем горба/желоба (при высоте соединенного седла на дереве изменений) | VolS | Указанный объем |
Площадь горба/желоба | Area | % области определения |
Окружность горба/желоба | Circ | Указанная длина |
6.4 Определение значимых характеристик
"Функция" взаимодействует со всеми характеристиками неодинаковым образом; различные характеристики взаимодействуют по-разному. Таким образом, принципиально различать те характеристики, которые имеют функциональную значимость, от функционально незначимых. Для каждой конкретной функции поверхности следует определить функцию сегментации, которая выявляет значимые и незначимые характеристики, определяемые сегментацией. Это набор значимых характеристик, используемых для описания. Методы определения значимых характеристик представлены в таблице 3. Все они относятся к функциям сегментации.
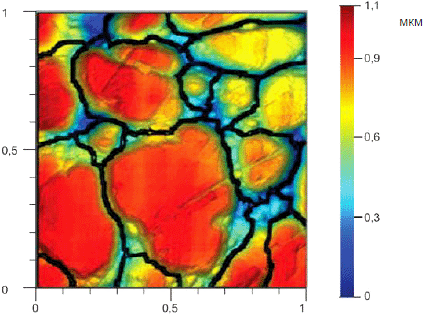
Рисунок 13 - Горбы, определенные при помощи отсечения Вольфа с использованием 10% Sz
Таблица 3 - Методы определения значимых характеристик
Класс характеристики | Метод определения значимых характеристик | Обозначение | Единицы измерения параметров |
Ареал | Характеристика ареала является значимой, если не связана с краем на данной высоте (см. рисунок 14, характеристика А). | Closed (закрыто) | Высота задана как коэффициент смятия/ |
Характеристика ареала является значимой, если связана с краем на данной высоте (см. рисунок 14, характеристика В). | Open (открыто) | Высота задана как коэффициент смятия | |
Точка | Пик является значимым, если он имеет один из показателей высоты максимального пика Вольфа N | Тор (сверху) | N - это целое число. |
Провал является значимым, если он имеет один из показателей высоты максимального провала Вольфа N | Bot (снизу) | N - это целое число. | |
Ареал, линия, точка | Использование всех характеристик | АII (все) | - |
Примечание 1 - Ожидается, что в будущих дополнениях к данной части ИСО 25178 будут представлены прочие стандартизированные методы определения функций сегментации для определенных функций.
Примечание 2 - Примеры закрытых горбов, открытых горбов и открытых желобов представлены на рисунке 14 с помощью поверхности на рисунке 12.
Примечание 3 - Определения закрытых горбов, открытых горбов и открытых желобов требуют дополнительного изучения для обеспечения их полной стабильности (в связи с "наличием/отсутствием соединения" с краем). Ожидается, что в будущих дополнениях к данной части ИСО 25178 будут определены стабильные версии данных концепций.
Условные обозначения: А - пример закрытого горба, т.е. не соединенного с краем (белый); В - пример открытого горба, т.е. соединенного с краем (черный); С - пример открытого желоба, т.е. соединенного с краем (серый).
Рисунок 14 - Горбы выше порога высоты (коэффициент смятия 50%), показаны соединенные с краем (черные) и не соединенные с краем горбы (белые)
6.5 Раздел показателей характеристик
После определения набора значимых характеристик необходимо определить соответствующие показатели характеристик для их описания. Большинство показателей отражают размер характеристики, например длину, площадь или объем характеристик. Некоторые показатели характеристик представлены в таблице 4.
Таблица 4 - Показатели характеристик
Класс характеристики | Показатели характеристик | Обозначение |
Ареал | Локальная высота пика/желоба | Lpvh |
Характеристика объема ареала (на высоте соединенного седла на дереве изменений) | VolS | |
Характеристика объема ареала (на высоте соединения с краем) | VolE | |
Характеристика площади ареала | AreaE | |
Характеристика окружности ареала | Cleng | |
Линия | Длина линии | Leng |
Точка | Локальная высота пика/желоба | Lpvh |
Локальная кривизна в критической точке | Curvature (кривизна) | |
Ареал, линия, точка | Показатель принимает значение единицы | Count (количество) |
Примечание - Ожидается, что в будущих дополнениях данной части ИСО 25178 будут представлены стандартизированные методы определения показателей характеристики для определенных функций.
6.6 Статистические параметры показателей
Заключительным этапом описания характеристики является расчет соответствующих статистических параметров показателей значимых характеристик, параметра характеристики или же гистограммы значений показателя. Некоторые статистические свойства показателей представлены в таблице 5.
Таблица 5 - Статистические параметры показателей
Статистический параметр показателя | Обозначение | Порог |
Арифметическое среднее значений показателей | Среднее значение | - |
Максимальное значение показателя | Мах | - |
Минимальное значение показателя | Min | - |
Среднеквадратичное значение показателя | RMS | - |
Процент вышеуказанного значения | Perc | Значение порога в единицах показателя |
Гистограмма | Hist | - |
Сумма значений показателей | Sum | - |
Сумма всех значений показателей, деленная на область определения | Density | - |
Примечание - Ожидается, что в будущих дополнениях к данной части ИСО 25178 будут представлены стандартизированные методы наименования определенных статистических параметров показателей.
6.7 Соглашение по описанию характеристик
Для регистрации описания характеристики необходимо показать специальные инструменты, использованные на каждом из пяти этапов. Этого можно достичь при помощи следующего соглашения.
- Начинать следует с букв FC, чтобы показать, что это описание характеристики.
- В свою очередь, для каждого этапа используют обозначение из соответствующей таблицы для указания необходимого инструмента.
- Некоторые инструменты этапа требуют дополнительных значений для полноты. Символ ";" используют для разделения этапов, а символ ":" - для разделений в пределах этапа.
- Если в данной части ИСО 25178 инструмент не указан, то вместо этого можно использовать ссылку на определение инструмента.
ПРИМЕР: FC;D;Wolfprune:5%;Edge:60%;AreaE;Hist.
6.8 Названные параметры характеристики
В терминологических записях, представленных ниже, за каждым термином следует его параметр (сокращенный термин), а затем его символ. И хотя сокращенные термины могут содержать множество букв, символ включает только одну букву с индексом (при необходимости). Символы используются в уравнениях, представленных в настоящем документе. Причина такого разделения состоит в том, чтобы избежать неправильной интерпретации составных букв как знака умножения между количественными параметрами в уравнениях. Параметры (сокращенные термины) используются в документации изделия, рисунках и листах технических данных.
6.8.1 плотность пиков Spd, Spd (density of peaks Spd, Spd): Число пиков на единицу площади
= FC;H;Wolfprune:X%;AII;Count;Density.
Примечание 1 - Условные обозначения представлены в таблицах 1-5.
Примечание 2 - Если не указано иное, значение X% по умолчанию представлено в ИСО 25178-3.
6.8.2 арифметическое среднее кривизны пика Spc, (arithmetic mean peak curvature Spc, Spc): Арифметическое среднее главной кривизны пиков в области определения
= FC;P;Wolfprune:X%;AII;Curvature;Mean.
Примечание 1 - Условные обозначения представлены в таблицах 1-5.
Примечание 2 - Если не указано иное, значение X% по умолчанию представлено в ИСО 25178-3.
6.8.3 высота поверхности по десяти точкам S10z, (ten-point height of surface S10z, S10z): Среднее значение высоты пяти пиков с наибольшей общей высотой пика плюс среднее значение высоты пяти провалов с наибольшей общей высотой провала в области определения
.
6.8.3.1 высота пика по пяти точкам S5p, (five-point peak height S5p, S5p): Среднее значение высоты пяти пиков с наибольшей общей высотой пика в области определения
= FC;H;Wolfprune:X%;Top:5;Lpvh;Mean.
Примечание 1 - Условные обозначения представлены в таблицах 1-5.
Примечание 2 - Если не указано иное, значение X% по умолчанию представлено в ИСО 25178-3.
6.8.3.2 высота провала по пяти точкам S5v, (five-point pit height S5v, S5v): Среднее значение высоты пяти провалов с наибольшей общей высотой провала в области определения.
= FC;D;Wolfprune:X%;Bot:5;Lpvh;Mean.
Примечание 1 - Условные обозначения представлены в таблицах 1-5.
Примечание 2 - Если не указано иное, значение X% по умолчанию представлено в ИСО 25178-3.
6.8.4 средняя площадь желоба Sda(c), 
(mean dale area Sda(c), Sda(c)):
= FC;D;Wolfprune:X%;Open:c/Closed:c;AreaE;Mean.
Примечание 1 - Условные обозначения представлены в таблицах 1-5. "Open:c/Closed:c" обеспечивает пользователю выбор "открыто при высоте с" или "закрыто при высоте с".
Примечание 2 - Если не указано иное, значение X% по умолчанию представлено в ИСО 25178-3.
Примечание 3 - Если не указано иное, значение "открыто/закрыто" представлено в ИСО 25178-3.
6.8.5 средняя площадь горба Sha(c), 
(mean hill area Sha(c), Sha(c)):
= FC;H;Wolfprune:X%;Open:c/Closed:c;AreaE;Mean.
Примечание 1 - Условные обозначения представлены в таблицах 1-5. "Open:c/Closed:c" обеспечивает пользователю выбор "открыто при высоте с" или "закрыто при высоте с".
Примечание 2 - Если не указано иное, значение X% по умолчанию представлено в ИСО 25178-3.
Примечание 3 - Если не указано иное, значение "открыто/закрыто" представлено в ИСО 25178-3.
6.8.6 средний объем желоба Sdv(c), 
: (mean dale volume Sdv(c), Sdv(c)):
= FC;D;Wolfprune:X%;Open:c/Closed:c;VolE;Mean.
Примечание 1 - Условные обозначения представлены в таблицах 1-5. "Open:c/Closed:c" обеспечивает пользователю выбор "открыто при высоте с" или "закрыто при высоте с".
Примечание 2 - Если не указано иное, значение X% по умолчанию представлено в ИСО 25178-3.
Примечание 3 - Если не указано иное, значение "открыто/закрыто" представлено в ИСО 25178-3.
6.8.7 средний объем горба Shv(c), 
(mean hill volume Shv(c) Shv(c)):
= FC;H;Wolfprune:X%;Open:c/Closed:c;VolE;Mean.
Примечание 1 - Условные обозначения представлены в таблицах 1-5. "Open:c/Closed:c" обеспечивает пользователю выбор "открыто при высоте с" или "закрыто при высоте с".
Примечание 2 - Если не указано иное, значение X% по умолчанию представлено в ИСО 25178-3.
Примечание 3 - Если не указано иное, значение "открыто/закрыто" представлено в ИСО 25178-3.
Приложение А
(справочное)
Сегментация
А.1 Сегментация поверхности
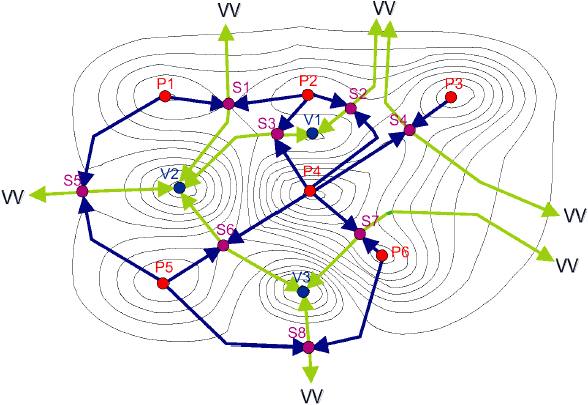
Более 100 лет назад Maxwell [12] предложил разделять ландшафт на области с горбами, а также области с желобами. Горб Максвелла - это область, от которой пути, направленные максимально вверх, ведут к одному определенному пику. Желоб Максвелла - это область, от которой пути, направленные максимально вниз, ведут к одному определенному провалу. По определению границами между горбами являются линии курса (русла), а границами между желобами - линии хребта (линии водораздела). Максвелл смог показать, что линии курса и линии хребта представляют собой пути, направленные максимально вверх и вниз, которые берут начало от точек седла и заканчиваются на пиках и в провалах. Недавно желоб Максвелла (линии водораздела) стали считать основным инструментом математической морфологии при сегментации изображения в процессе подготовки к распознаванию образа.
К сожалению, сегментация поверхности или изображения на желоба Максвелла нередко не оправдывает надежд, поскольку поверхность/изображение чрезмерно сегментируется на большое число незначительных мелких неглубоких желобов, а не на несколько значительных крупных и глубоких желобов. Все, что необходимо - объединить незначимые желоба в более крупные значимые желоба.
Предложено расширить определения Максвелла и определить желоб как один доминирующий провал, окруженный кольцом из линий хребта, которые соединяют пики и точки седла. Кроме того, горб определяется как один доминантный пик, окруженный кольцом из линий курса, соединяющих провалы и точки седла. В желобе или горбе могут находиться прочие провалы/пики, однако все они будут незначимы по сравнению с доминантным провалом/пиком.
Желоб - это ареал, эквивалентный мотиву профиля (см. ИСО 12085). Горб - это также полезное дополнительное понятие. По аналогии с мотивом профиля горбы и желоба характеризуются несколькими типами специфических точек и линий поверхности. Они включают критические точки (пики, провалы и точки седла), а также критические линии (линии хребта и линии курса), (см. рисунок А.1).
Также важно учитывать эффекты края. Принцип (бритва) Оккама (non sunt multiplicanda entia praeter neces-sitatem - объекты не подлежат умножению сверх необходимости) используется для распространения контурных линий за пределы представляющей интерес области таким образом, чтобы было создано минимальное число новых критических точек. Принцип Оккама ведет к двум возможным решениям, названным "виртуальным провалом" и "виртуальным пиком", каждый является двойником другого. Принята концепция виртуального провала [13]. Предполагается, что виртуальный провал - это точка высоты за вычетом бесконечности, с которой соединены все точки границы. (Предполагается, что виртуальный пик - это точка бесконечной высоты, с которой соединены все точки границы).
А.2 Сочетающиеся сегменты
А.2.1 Дерево изменений
Полезным методом организации связей между критическими точками в горбах и желобах с сохранением важной информации является дерево изменений. Kweon и Kanade [14] предложили концепцию дерева изменений ограниченного масштаба для описания возможности соединения поверхности. Дерево изменений отражает связь между контурными линиями от поверхности и является одним примерном* более общего топологического объекта, названного графиком Reeb [13]. Вертикальное направление на дереве изменений соответствует высоте. При заданной высоте все индивидуальные контурные линии представлены точкой. Последняя является частью линии, отражающей тот факт, что контурная линия непрерывно изменяется в зависимости от высоты. Точки седла представлены объединением двух или более таких линий в одну; пики и провалы представлены прекращением линии.
_______________
* Текст документа соответствует оригиналу. - .
Условные обозначения: Р - пики; V - провалы; S - точки седла; VV - виртуальный провал.
Рисунок А.1 - Контурная карта, на которой представлены критические линии и точки
Представим себе постепенное заполнение желоба водой. Точка, в которой вода сначала вытекает из желоба, - это точка седла. Провал в желобе соединен с данной точкой седла в дереве изменений. При продолжении заполнения нового озера следующая точка, в которой вода вытекает из озера, также является точкой седла. И снова линия на дереве изменений, отражающая контур береговой линии озера, будет соединена с данной точкой седла в дереве изменений. Данный процесс может продолжаться и определяет соединение между провалами, точками седла и деревом изменений. После переворота ландшафта таким образом, чтобы пики стали провалами и т.д., сходный процесс сформирует соединение между пиками, точками седла и деревом изменений.
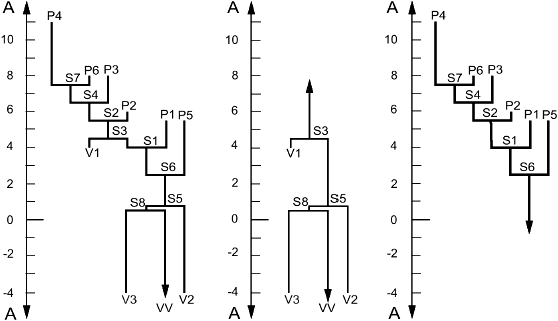
Существует по меньшей мере три типа дерева изменений:
- дерево полного изменения, которое отражает связь между критическими точками в горбах и желобах (рисунок А.2);
- дерево изменения желоба, которое отражает связь между провалами и точками седла (рисунок А.3);
- дерево изменения горба, которое отражает связь между пиками и точками седла (рисунок А.4).
Условные обозначения: А - высота, мкм; Р - пики; V - провалы; S - точки седла; VV - виртуальный провал
Рисунок А.2 - Полное дерево изменений | Рисунок А.3 - Дерево изменений желоба | Рисунок А.4 - Дерево изменений горба |
Следует отметить, что дерево изменений желоба и горба может рассчитываться на основании полного дерева изменений. В остальной части данного приложения под "деревом изменений" подразумевает полное дерево изменений.
А.2.2 Комбинация ареала
На практике дерево изменений может изобиловать очень короткими контурными линиями из-за шума и т.д., что мешает интерпретации (избыточная сегментация поверхности/изображения горбами и желобами Максвелла). Необходим механизм отсечения дерева изменений, который снижает шум, но оставляет важную информацию. Таким механизмом является комбинация ареала; это упрощает дерево изменений, сохраняя при этом важную информацию.
А.2.3 Правила комбинации ареала
Ниже представлено описание алгоритма комбинации ареала для полного дерева изменений. Данный алгоритм может быть легко изменен для комбинаций желоба или горба, поэтому данные случаи не будут здесь обсуждаться. Представленный здесь упрощенный алгоритм предполагает наложение условий виртуального провала.
Этап 1: предполагая условия виртуального провала, ищут все горбы и желоба Максвелла, формируя полное дерево изменений.
Этап 2: классифицируют все пики, провалы, края пиков и края провалов на значимые или незначимые согласно функции поверхности.
Этап 3: комбинируют незначимые пики и провалы с прилегающей точкой седла, с которой они соединены в дереве изменений.
Полученное дерево изменений будет отражать значимые пики, провалы, краевые пики и краевые провалы, а также связи между ними. Таким образом, дерево изменений подрезали, снижая шум, но сохраняя важную информацию.
А.2.4 Какие сегменты подлежат комбинации
Функция сегментации включает расщепление набора "явлений" на два отдельных набора, названных "значимыми явлениями" и "незначимыми явлениями". Чтобы функция сегментации давала уникальные и стабильные результаты, она должна удовлетворять следующим трем требованиям [20]:
- Р1: Каждое явление относят к одному и только одному набору из двух перечисленных (т.е. наборы значимых и незначимых явлений).
- Р2: Если значимое явление удалить из набора явлений, то остальные значимые явления сохраняются в новом наборе значимых явлений.
- Р3: Если незначимое явление удалить из набора явлений, получается аналогичный перечень значимых явлений.
Можно показать, [16], что все функции сегментации, которые удовлетворяют данным трем требованиям, могут быть представлены на схеме в соотношении один к одному в определенной подгруппе морфологических закрывающих фильтров. Морфологические закрывающие фильтры широко используются при анализе изображений. Они представляют собой агрегирующие функции со следующими тремя определяющими свойствами [17]:
a) Все множества представляют собой подмножества с собственным замыканием;
b) Замыкание замыкания множества - замыкание оригинального множества;
c) Замыкание подмножества - подмножество замыкания оригинального множества.
Конкретное подмножество закрывающих фильтров, на которые картируют функции сегментации, - закрывающие фильтры со следующими свойствами.
Если два набора явлений обеспечивают одно и то же за, то их пересечение также дает аналогичное закрытие.
Любое закрытие, которое удовлетворяет данному требованию, может быть картировано в соотношении один к одному на определенной функции сегментации следующим образом.
Для любого набора явлений рассматривают наименьший поднабор данного набора, который дает аналогичное закрытие с оригинальным набором явлений. Можно показать, что данный поднабор уникален, хорошо определен и соответствует набору значимых явлений, а его дополнение с точки зрения набора явлений соответствует набору незначимых явлений. Также хорошо определено обратное картирование. Доказательство данных результатов представлено в ссылке [16].
Этот важный результат позволяет создавать все возможные функции комбинации сегментаций от фильтров морфологического закрытия, свойства которых очень хорошо известны, включая способ получения всех возможных конечных закрывающих фильтров [17].
А.3 Отсечение ветвей дерева изменений
А.3.1 Общие сведения
В современной литературе имеется несколько опубликованных ссылок на методы, аналогичные отсечению ветвей дерева изменений (см. ссылки [18], [19] и [20]).
Wolf [18] представляет метод, эквивалентный отсечению ветвей дерева изменений. Это обсуждается в разделе А.3.2.
Совсем недавно в литературе появились методы слияния водоразделов (желобов Максвелла) [19], [20]. Слияние водоразделов эквивалентно отсечению ветвей дерева изменений лишь в том случае, если предполагается, что триангуляция реберной решетки представляет собой непрерывную поверхность (т.е. треугольные фасетки).
Показано, что все указанные выше методы отсечения удовлетворяют свойствам, представленным в разделе А.2.4.
А.3.2 Отсечение по Вольфу
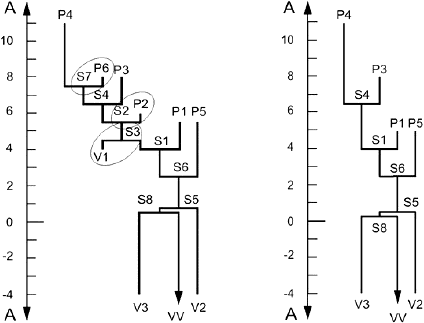
Сначала для каждого пика и провала рассчитывают различие высоты между пиком или провалом и соседней точкой седла, с которой они соединяются на дереве изменений. Метод отсечения Вольфа включает поиск пика или провала с наименьшим различием высоты и соединение его с соседней точкой седла на дереве изменений. Другой пик или провал, который также соединен с данной точкой седла, соединяют с другим седлом; его отличие по высоте корректируют для отражения данного факта. Затем процесс повторяют в отношении пика или провала с наименьшим различием по высоте с прилегающей точкой седла не дереве изменений, которую устраняют до достижения некоторого порога. Данный порог достигается в том случае, когда все оставшиеся различия высоты превышают фиксированное значение, либо когда остается фиксированное число пиков или провалов. Можно легко доказать, что оба критерия ведут к функции сегментации, которая удовлетворяет трем необходимым свойствам, представленным в пункте А.2.4. При помощи дерева изменений, представленного на рисунке А.2, все элементы P6-S7, P2-S2 и V1-S3 принимают значение наименьшей разницы по высоте, т.е. 0,5. Их отсечение дает дерево изменений, представленное на рисунке А.5.
Использование отсечения Вольфа до тех пор, пока на поверхности не останется пять пиков или пять провалов, обеспечивает стабильное определение параметра высоты по 10 точкам. Данные пики/провалы могут не быть максимальными/минимальными, но они будут самыми высокими.
Примечание - вершина горы Эверест может быть на максимальной высоте на земле, но гора не является самой высокой (от основания до пика). Данный рекорд принадлежит горе Мауна Кеа на Гавайях.
а) До отсечения б) После отсечения
Условные обозначения: А - высота, мкм; Р - пики; V - провалы; S - точки седла; VV - виртуальный провал.
Рисунок А.5 - Отсечение Вольфа для рисунка А.2
Приложение В
(справочное)
Фрактальные методы
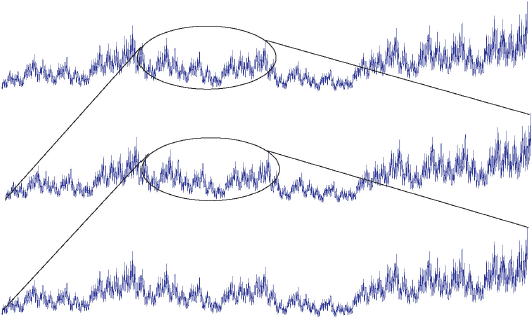
В.1 Что такое фрактал?
Фрактал - это объект, который выглядит примерно одинаково в определенном диапазоне масштабов или увеличения, т.е. объект должен быть статистически подобен самому себе, см. рисунок Б.1. Объект не должен демонстрировать точно такую же структуру при всех масштабах, однако аналогичный "тип" структуры должен появляться в некотором диапазоне масштабов.
Рисунок В.1 - Фрактальный профиль демонстрирует аналогичные структуры при всех масштабах
В целом, "размер фрактала" можно рассчитать из поверхности фрактала при помощи различных методов, [21], [22], включая метод изменчивости [23] и анализ относительной площади [24]. Последний метод способен давать параметры, имеющие сильные функциональные связи с адгезией [25], электрохимическим импедансом [26], трением [27], блеском [28], хорошим разделением зубчатого микроизноса [29], условиями шлифования [30], переносом массы при нагреве [31], а также прессованным порошком [32].
Фрактальный размер - это показатель геометрической сложности или сложности компонентов фрактала либо частично фрактальной поверхности. Фрактальные размеры увеличиваются по мере увеличения сложности. Фрактальный размер больше или равен евклидову размеру, т.е. больше или равен 1 и меньше 2 для профиля, а также больше или равен 2 и меньше 3 для поверхности.
Реальные поверхности являются частично фрактальными по той причине, что могут быть охарактеризованы, аппроксимированы или смоделированы как имеющие геометрические компоненты неправильной формы в определенном диапазоне масштабов наблюдений. Идеальные фрактальные поверхности - математические модели, имеющие неправильные компоненты при всех масштабах наблюдения.
Периодические и квазипериодические геометрические компоненты поверхности не исключают наличия компонентов фрактала на данной поверхности, а также ее успешное описание методом фрактального анализа.
В.2 Методы изменчивости
Пусть F(s) будет объемом между конвертом морфологического закрытия и конвертом морфологического открытия поверхности фрактала с квадратным структурным элементом горизонтальной плоскости с масштабом s (s по s).
Тогда, при условии существования пределов,
.
Размер фрактала, рассчитанный при помощи метода изменчивости, эквивалентен размеру Minkowski-Bouligand. Показано [23], что метод изменчивости имеет наименьшую неопределенность по сравнению со всеми современными методами для расчета размера фрактала. Фрактальный размер поверхности больше или равен двум и отражает сложность фрактальной поверхности. Чем больше размер фрактала, тем более сложной или неправильной является фрактальная поверхность.
В.3 Метод изменчивости, применяемый к поверхности ограниченного масштаба
В строгом математическом смысле поверхности ограниченного масштаба не являются истинной фрактальными, поскольку имеют умышленно слаженную поверхность при некотором определенном масштабе, поэтому не содержат "подобных структур при всех масштабах". Вместе с тем, поверхности ограниченного масштаба могут демонстрировать "поведение по типу фрактала" в диапазоне масштабов. График масштаба-объема (представленный на рисунке В.2) очень помогает в регистрации некоторых вариантов такого поведения в наблюдаемом диапазоне масштабов.
График масштаба-объема Svs(s) представляет собой график логарифма объема между конвертами морфологического закрытия и открытия поверхности ограниченного масштаба при помощи квадратной горизонтальной плоскости в качестве структурного элемента в зависимости от логарифмической шкалы структурного элемента.
Условные обозначения: X - масштаб, в мкм; Y - объем, в кубических мкм; а - масштаб; b - объем.
Рисунок В.2 - График масштаба-объема для поверхности ограниченного масштаба
Большинство графиков масштаба-объема для поверхности ограниченного масштаба будут отражать несколько областей, в которых кривая представляют собой приблизительно прямую линию. В каждой из этих определенных областей связь между масштабом s и объемом 
приобретает форму
.
Это степенной закон, поскольку объем 
изменяется по аналогии со степенью масштаба s. Угол наклона прямой линии, на графике масштаба-объема, представляет собой просто экспоненту d, а ее отрезок объема - log(с).
В этих диапазонах масштабов, где действует определенный степенной закон (т.е. в соответствующем диапазоне графика масштаба-объема, где кривая приблизительно соответствует прямой линии), поверхность ограниченного масштаба будет самоподобна (т.е. части поверхности после соответствующего увеличения будут выглядеть как оригинальная поверхность). Таким образом, поверхность ограниченного масштаба в определенном диапазоне масштабов приблизительно представляет собой фрактальную поверхность с размером фрактала 2+d. Таким образом, чем более крутым является угол наклона графика масштаба-объема, тем более сложна поверхность для данного определенного диапазона масштабов.
Как уже было указано выше, большинство графиков масштаба-объема будут иметь несколько областей, где кривая приблизительно соответствует прямой линии. Масштаб, при котором отмечают изменение угла наклона от одной области, аппроксимируемой прямой линией, к другой области называют "масштабом перекреста". На практике возможно постепенное изменение. По этой причине необходима процедура для определения масштаба, при котором происходит изменение. Определение масштабов перекреста важно по той причине, что они отражают изменение основного механизма, влияющего на поверхность ограниченного масштаба, и/или процедуры оценки. Пример представлен на рисунке В.3. При перекресте от сравнительно больших масштабов, где угол наклона близок к нулю, к меньшим масштабам, где наклон круче, первый масштаб перекреста свидетельствует об изменении от сравнительно гладкой поверхности при более крупных масштабах к более шероховатой поверхности при мелких масштабах. Таким образом, на уровне выше данного первого масштаба перекреста определенная эта поверхность ограниченного масштаба может рассматриваться как гладкая.
Условные обозначения: X - масштаб, в мкм; Y - объем, в кубических мкм; а - масштаб первого перекреста; b - масштаб второго перекреста.
Рисунок В.3 - Теоретический график объема-масштаба, демонстрирующий масштабы перекреста
В.4 Анализ относительной площади
Любой размер D поверхности, фрактальной или евклидовой, можно представить в виде отношения логарифма числа элементов ареала N к логарифму обратного отношения линейного масштабирования, r [33]
D=(logN)/[log(1/r)].
Для идеальной фрактальной поверхности представленное выше уравнение отражает угол наклона дважды логарифмического графика относительной площади, поскольку охвачены все масштабы, включая r = 1 (в этой точке N также равно 1). Для реальных поверхностей данное правило, как правило, неверно. На реальных поверхностях фрактальные размеры рассчитывают по углу наклона данных графиков в диапазоне масштаба, в котором поверхность является самоподобной.
Наблюдаемая площадь измеренной поверхности рассчитывается как функция масштаба в серии виртуальных отсечений с охватом измеренной поверхности в лоскутном режиме [24], [34]. Области плиток, или фрагментов, представляют масштабы ареала наблюдения. Отсечения повторяют с плитками постепенно уменьшающейся площади для определения наблюдаемых площадей как функции масштабов ареала наблюдения (рисунок В.4) [34].
А=1270000 нм | 72 В | С=1,052 |
| ||
А=263000 нм | 409 В | С=1,181 |
| ||
А=52900 нм | 2416 В | С=1,33 |
| ||
А=7830 нм | 18331 В | С=1461 |
| ||
Условные обозначения: А - масштаб; В - элемент мозаичного изображения; С - относительная площадь. Размер треугольной плитки, или фрагментов, представленный в описании, представляет собой масштаб наблюдения. Номинальные показатели площади, покрываемые при каждом приеме фрагментации изображения, представлены сверху каждой ячейки.
Рисунок В.4 - Четыре приема фрагментации изображения по данным анализа относительной площади
Наблюдаемая площадь - это число плиток, или фрагментов, для одного виртуального приема по фрагментации, умноженное на площадь плитки, или фрагмента (т.е. масштаб наблюдения). Например, измеренная площадь составляет 18331 плитка х 7830 нм= 143531730 нм
при масштабе 7830 нм
. Наблюдаемая площадь - это явная площадь в определенном масштабе наблюдения, которая должна иметь ссылку на этот масштаб, поскольку наблюдаемая площадь меняется в зависимости от масштаба наблюдения. Номинальная площадь - это площадь одного приема фрагментации изображения с проекцией на номинальную поверхность, т.е. площадь на номинальной поверхности, покрытая за один прием фрагментации. Для номинальной поверхности может использоваться плоскость наименьших квадратов или данные измерения. Относительная площадь - это наблюдаемая площадь в определенном масштабе, деленная на номинальную площадь [25], [34]. Следовательно, минимальная относительная площадь равна единице.
График относительной площади - это билогарифмический график относительных площадей в зависимости от масштаба наблюдения (рисунок В.5). Размер D в определенном диапазоне масштаба может рассчитываться по углу наклона b графика относительной площади следующим образом
D=2 - 2b,
что может быть показано как производное предыдущего уравнения для D.
Условные обозначения: X - масштаб наблюдений (нм); Y - относительная площадь;
Угол наклона. Фрактальный размер составляет около 2,144.
Рисунок В.5 - График относительной площади, включая результаты серийной фрагментации изображений на рисунке В.4
Приложение С
(справочное)
Основы для стандартов структуры поверхности ареала
С.1 График событий
Ниже представлен график событий, приведших к публикации данной серии Международных стандартов по структуре поверхности ареала.
Апрель 1990 года - апрель 1993 года | Финансируемый ЕС проект под названием "Разработка методов для изучения шероховатости в трех измерениях" под руководством Бирмингемского университета. Разработана основа для изучения структуры поверхности ареала. Отчет по проекту |
Сентябрь 1993 года | Опубликована "Синяя книга" [21] с подробными результатами представленного выше проекта ЕС. Данная книга стала фактически стандартом для изучения структуры поверхности ареала. |
Апрель 1998 года - апрель 2001 года | Проект AUTOSURF под руководством университета Ровера/Брунеля. В данном проекте, спонсируемом ЕС, разработаны методы изучения структуры поверхности ареала для листовых материалов для автомеханического использования. Сюда относится изучение удержания масла во время хранения колец, характеристик давления и окраски. Использован инструмент "характеристика" для решения проблем структуры реальной поверхности. |
Май 1998 года - май 2001 года | Проект SURFSTAND под руководством Университета Хаддерсфилда. Данный спонсируемый ЕС проект заложил основу для стандартизации анализа структуры поверхности ареала. В серии отдельных исследований оценивалась функциональная пригодность параметров "Birmingham 14". Определения структуры ареала были пересмотрены, что привело к созданию "более строгих" определений параметров "поля" и введению инструмента "характеристика". Разработаны устойчивых технологий* и технологий вейвлет-фильтра. Наконец, изучены вопросы, связанные с калибровкой инструмента ареала. |
___________________ * Текст документа соответствует оригиналу. - . | |
Январь 2002 года | Презентации проектов SURFSTAND и AUTOSURF перед техническими комитетами ИСО/ТС 213 в Мадриде, Испания. |
Июнь 2002 года | Технические комитеты ИСО/ТС 213 учредили рабочую группу по структуре поверхности для определения требований к стандартизации структуры поверхности ареала. |
Январь 2003 года | Технические комитеты ИСО/ТС 213 учредили новую Рабочую группу WG 16 для разработки новой системы структуры поверхности в рамках следующего поколения GPS. |
Май 2003 года | Опубликована "Зеленая книга" [11] с подробными результатами проекта SURFSTAND. |
Июнь 2003 года | Опубликован ASME В46.1-2003. Содержит основы фрактальных методов оценки структуры поверхности ареала, а также классификацию инструментов для структуры поверхности. |
С.2 Ссылки по предмету
Ссылки, используемые в данной серии Международных стандартов по структуре поверхности ареала, представлены в библиографии. Ссылки, не соответствующие ИСО, отсортированы по полю предмета.
Приложение D
(справочное)
Диаграммы концепции
D.1 Общие термины
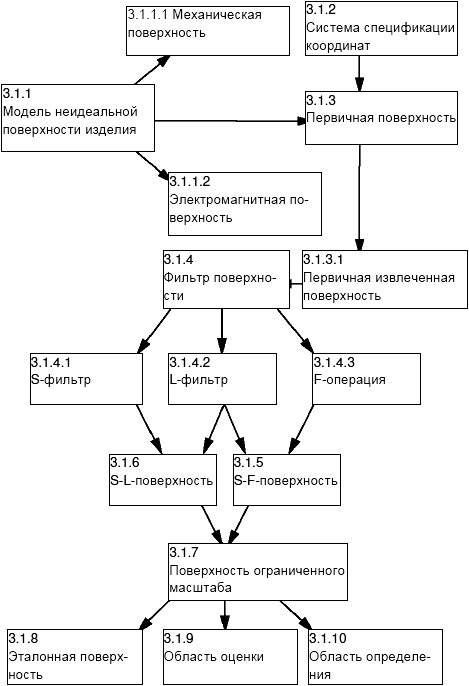
D.2 Термины геометрических параметров
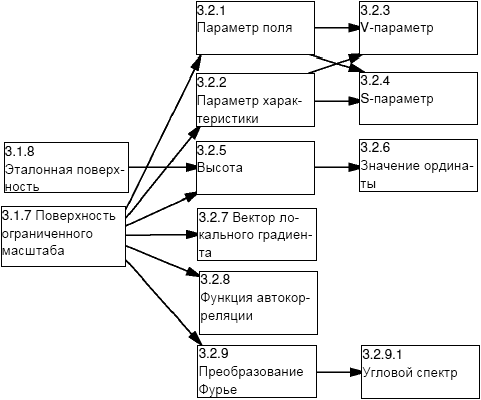
D.3 Термины геометрических характеристик
D.3.1 Характеристики
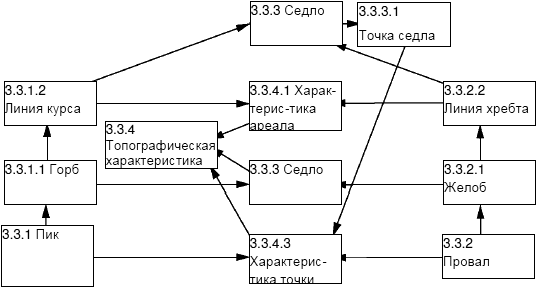
D.3.2 Анализ характеристик
Приложение Е
(справочное)
Связь с матричной моделью геометрических характеристик изделий (GPS)
Е.1 Общие данные
Все подробные сведения о матричной модели GPS представлены в ИСО/TR 14638.
ИСО/GPS Основная схема, представленная в ИСО/TR 14638, содержит обзор системы ИСО/GPS, частью которой является данный документ. Фундаментальные правила ИСО/GPS, представленные в ИСО 8015, применимы к данному документу, а правила принятия решений по умолчанию, представленные в ИСО 14253-1, применимы к спецификациям, составленным в соответствии с настоящим документом, если не указано иное.
Е.2 Информация о настоящем документе и его использовании
Данная часть ИСО 25178 устанавливает термины, определения и параметры для оценки структуры поверхности (шероховатость, волнистость и первичная поверхность) ареальными методами.
Е.3 Расположение в матричной модели GPS
Настоящая часть ИСО 25178 представляет собой общий стандарт GPS, который влияет на 2-е звено цепочек стандартов по структуре поверхности в матричной структуре GPS, что графически представлено на рисунке Д.1*.
_____________
* Вероятно ошибка оригинала. Следует читать: на рисунке Е.1. - .
Фундаментальные стандарты GPS | Глобальные стандарты GPS | ||||||
Общая матрица GPS | |||||||
Номер звена цепи | 1 | 2 | 3 | 4 | 5 | 6 | |
Размер | |||||||
Расстояние | |||||||
Радиус | |||||||
Угол | |||||||
Форма линии, независимой от данных | |||||||
Форма линии, зависимой от данных | |||||||
Форма поверхности, независимой от данных | |||||||
Форма поверхности, зависимой от данных | |||||||
Ориентация | |||||||
Расположение | |||||||
Круговой прогон | |||||||
Полный прогон | |||||||
Данные | |||||||
Профиль шероховатости | |||||||
Профиль волнистости | |||||||
Первичный профиль | |||||||
Недостатки поверхности | |||||||
Края | |||||||
Структура поверхности ареала | |||||||
Рисунок Е.1 Расположение в матричной модели GPS
Е.4 Связанные международные стандарты
Связанные стандарты относятся к цепям стандартов, представленных на рисунке Е.1.
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам Российской Федерации
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ИСО/TS 16610-1:2006 | - | * |
ИСО 17450-1:2011 | - | * |
ИСО 25178-3:- | - | * |
* Соответствующий национальный стандарт отсутствует. До его утверждения рекомендуется использовать перевод на русский язык данного международного стандарта. Перевод данного международного стандарта находится в Федеральном информационном фонде технических регламентов и стандартов. | ||
Библиография
[1] | ISO 8015, Geometrical product specifications (GPS) - Fundamentals - Concepts, principles and rules (ИСО 8015, Геометрические характеристики изделий (GPS). Основные принципы. Концепции, принципы и правила). |
[2] | ISO 11562, Geometrical Product Specifications (GPS) - Surface texture: Profile method - Metrological characteristics of phase correct filters (ИСО 11562 Геометрические характеристики изделий (GPS). Структура поверхности. Профильный метод. Метрологические характеристики фильтров с коррекцией фазы). |
[3] | ISO 12085:1996, Geometrical Product Specifications (GPS) - Surface texture: Profile method - Motif parameters (ИСО 12085:1996, Геометрические характеристики изделий (GPS). Структура поверхности. Профильный метод. Параметры мотива). |
[4] | ISO 13565-2:1996, Geometrical Product Specifications (GPS) - Surface texture: Profile method; Surfaces having stratified functional properties - Part 2: Height characterization using the linear material ratio curve (ИСО 13565-2:1996, Геометрические характеристики изделий (GPS). Структура поверхности. Профильный метод. Поверхности с послойным распределением функциональных свойств. Часть 2. Описание высот с помощью кривой коэффициента смятия). |
[5] | ISO 13565-3:1998, Geometrical Product Specifications (GPS) - Surface texture: Profile method; Surfaces having stratified functional properties - Part 3: Height characterization using the material probability curve (ИСО 13565-3:1998, Геометрические характеристики изделий (GPS). Структура поверхности. Профильный метод. Поверхности с послойным распределением функциональных свойств. Часть 3. Описание высот с помощью кривой распределения материала). |
[6] | ISO 14406:2010, Geometrical product specifications (GPS) - Extraction (ИСО 14406:2010, Геометрические характеристики изделий (GPS). Выдержки). |
[7] | ISO/TR 14638, Geometrical product specification (GPS) - Masterplan (ИСО/TR 14638, Геометрические характеристики изделий (GPS). Основная схема). |
[8] | ISO/TS 16610-20:2006, Geometrical product specifications (GPS) - Filtration - Part 20: Linear profile filters: Basic concepts (ИСО/TS 16610-20:2006, Геометрические характеристики изделий (GPS). Фильтрация. Часть 20. Фильтры линейного профиля. Основные понятия). |
[9] | ISO 25178-3, Geometrical product specifications (GPS) - Surface texture: Areal - Part 3: Specification operators (ИСО 25178-3, Геометрические характеристики изделий (GPS). Структура поверхности. Ареал. Часть 3. Операторы спецификаций). |
Ссылки, связанные с параметрами поля | |
[10] | STOUT, K.J. et al. The development of methods for the characterisation of roughness in three dimensions. European Report EUR 15178 EN, ISBN 0 7044 1313 2 |
[11] | BLUNT, L. and JIANG, X. Advanced techniques for assessment surface topography - Development of a basis for the 3D Surface Texture Standards "SURFSTAND", Kogan Page Science, ISBN 1903996112, 2003 |
Ссылки, связанные с параметрами характеристик См. ссылку [11] и следующие документы. | |
[12] | MAXWELL, J.C. On hills and dales. The London, Edinburgh, and Dublin Phil. Mag. and J. Sci., Series 4, 40, 1870, pp. 421-425 |
[13] | TAKAHASHI, S. et al. Algorithms for extracting correct critical points and constructing topological graphs from discrete geographical elevation data. Computer Graphics Forum, 14 (3), 1995, pp. C181-C192 |
[14] | KWEON, I.S. and KANADE, T. Extracting topographic terrain features from elevation maps, CVGIP: image understanding, 59 (2), 1994, pp. 171-182 |
[15] | SCOTT, P.J. The Mathematics of motif combination and their use for functional simulation. Int. J. Mech. Tools Manufact., 32 (1-2), 1992, pp. 69-73 |
[16] | SCOTT, P.J. Pattern Analysis and Metrology: The extraction of stable features from observable measurements. Proc. R. Soc. Lond. A, 460, 2004, pp. 2845-2864 |
[17] | SERRA, J. and VINCENT, L. An Overview of Morphological Filtering. Circuits, Systems, and Signal Processing, 11 (1), 1992, pp. 47-108 |
[18] | WOLF, G.W. A Fortran subroutine for cartographic generalization. Computers and Geoscience, 17 (10), 1991, pp. 1359-1381 |
[19] | BLEAU, A. and LEON, L.J. Watershed-based segmentation and region merging. Computer Vision and Image understanding, 77, 2000, pp. 317-370 |
[20] |
|
Ссылки, связанные с фрактальными методами | |
[21] | DECHIFFRE, L., LONARDO, Р. et al. Quantitative Characterisation of Surface Texture. Annals of the CIRP, 49 (2), 2000, pp. 635-652 |
[22] | JOHNSEN, W.A. and BROWN, C.A. Comparison of Several Methods for Calculating Fractal-Based Topographic Characterization Parameters. Fractals, 2/3, 1994, pp. 437-440 |
[23] | DUBUC, B., ZUCKER, S.W. et al. Evaluating the Fractal Dimension of Surfaces. Proc. R. Soc. Lond. A, 425, 1989, pp. 113-127 |
[24] | BROWN, C.A., CHARLES, P.D. et al. Fractal Analysis of Topographic Data by the Patchwork Method. Wear, 161, 1993, pp. 61-67 |
[25] | BROWN, C.A. and SIEGMANN, S. Fundamental scales of adhesion and area-scale fractal analysis. Int. J. Mech. Tools Manufact., 41, 2001, pp. 1927-1933 |
[26] | MCRAE, G.A. et al. Atomic Force Microscopy of Fractal Anodic Oxides on Zr-2.5Nb. J. of Applied Surface Science, 191 (1-4), 2002, pp. 94-105 |
[27] | JOHNSEN, W.A. Advances in the design of pavement surfaces. PhD dissertation, Worcester Polytechnic Institute, Worcester, Massachusetts, USA, 1997 |
[28] | BRIONES, V. et al. Scale-sensitive fractal analysis of the surface roughness of bloomed Chocolate. J. American Oil Chemists Society, 83 (3), 2006, pp. 193-199 |
[29] | SCOTT R.S., UNGAR P.S. et al. Dental microwear texture analysis within-species diet variability in fossil hominins. Nature, 436 (4), 2005, pp. 693-695 |
[30] | JORDAN, S.E. and BROWN, C.A. Comparing texture characterization parameters on their ability to differentiate ground polyethylene ski bases. Wear, 261 (3-4), 2006, pp. 398-409 |
[31] | KARABELCHTCHIKOVA, O., BROWN, C.A. et al. Effect of surface roughness on kinetics of mass transfer during gas carburizing. International Heat Treatment and Surface Engineering, 1/4, 2007 |
[32] | NARAYAN, P. and HANCOCK, B. Using fractal analysis to differentiate the surface topography of various pharmaceutical excipient compacts. Materials Science and Engineering, A: Structural Materials: Properties, Microstructure and Processing, 430 (1-2), 2006, pp. 79-89 |
[33] | MANDELBROT, B.B. Fractals: Form, Chance and Dimension. W. H. Freeman and Co., New York, 1977 |
[34] | ASME B46.1-2003, Surface Texture, Surface Roughness, Waviness and Lay |
Прочие методы | |
[35] | BURROWS, J.M. and GRIFFITHS, B.J. A vector modelling technique for the representation of 3- dimensional surface topography. Int. J. Mech. Tools Manufact., 38, 1998, pp. 537-542 |
Исследования случаев | |
См. ссылку [11]. |
, F. and LOPEZ, J. Watershed lines and catchment basins: a new 3D-motif method. Int. J. Mech. Tools Manufact., 40, 2000, pp. 1171-1184УДК | 620.1.08:62-408 | ОКС 17.040.20 |
Ключевые слова: имплантаты, геометрические характеристики изделий, структура поверхности, профильный метод, параметры структуры поверхности, профиль, пик профиля, впадина профиля | ||
Электронный текст документа
и сверен по:
, 2015
